
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1309 Атанасян — Подробные Ответы
Докажите, что плоскость, проходящая через ребро и середину противоположного ребра тетраэдра, разделяет его на две части, объёмы которых равны.
Точка \(E\) — середина \(BC\) (\(BE = EC\)), поэтому \(S_{AEB} = S_{AEC}\). Высота обеих пирамид \(DAEB\) и \(DAEC\) равна \(h\) (общая высота тетраэдра). Объемы вычисляются по формуле \(V = \frac{1}{3}Sh\):
\[
V_{DAEB} = \frac{1}{3}S_{AEB} \cdot h = \frac{1}{3}S_{AEC} \cdot h = V_{DAEC}.
\]
Равенство объемов доказано.
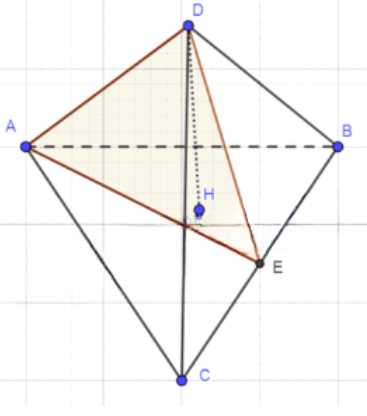
Дано тетраэдр \(DABC\) с точкой \(E\) на ребре \(BC\) такой, что \(BE = EC\). Плоскость \(ADE\) является сечением. Требуется доказать, что объемы пирамид \(DAEC\) и \(DAEB\) равны: \(V_{DAEC} = V_{DAEB}\).
Доказательство начинается с рассмотрения основания тетраэдра — треугольника \(ABC\). Поскольку \(E\) — середина \(BC\) (по условию \(BE = EC\)), отрезок \(AE\) является медианой. Медиана делит треугольник на два равновеликих треугольника \(AEB\) и \(AEC\), так как их высоты, опущенные из вершины \(A\), совпадают, а основания \(BE\) и \(EC\) равны. Таким образом, площади этих треугольников равны: \(S_{AEB} = S_{AEC} = \frac{1}{2}S_{ABC}\).
Далее, рассмотрим высоту тетраэдра \(DABC\) — отрезок \(DH\), перпендикулярный плоскости основания. Обозначим длину этой высоты как \(h\). Поскольку пирамиды \(DAEB\) и \(DAEC\) имеют общую вершину \(D\) и их основания \(AEB\) и \(AEC\) лежат в одной плоскости, их высоты также равны \(h\).
Теперь вычислим объемы этих пирамид. Объем пирамиды вычисляется по формуле \(V = \frac{1}{3} \cdot S_{\text{осн}} \cdot h\). Для пирамиды \(DAEB\) получаем: \(V_{DAEB} = \frac{1}{3} \cdot S_{AEB} \cdot h\). Аналогично для пирамиды \(DAEC\): \(V_{DAEC} = \frac{1}{3} \cdot S_{AEC} \cdot h\).
Подставляя ранее доказанное равенство площадей \(S_{AEB} = S_{AEC}\), приходим к равенству объемов: \(V_{DAEB} = \frac{1}{3} \cdot S_{AEB} \cdot h = \frac{1}{3} \cdot S_{AEC} \cdot h = V_{DAEC}\).
Таким образом, \(V_{DAEC} = V_{DAEB}\), что и требовалось доказать.
В решении использованы следующие ключевые моменты:
1. Свойство медианы делить треугольник на две равновеликие части.
2. Формула объема пирамиды через площадь основания и высоту.
3. Равенство высот пирамид \(DAEB\) и \(DAEC\), так как их основания лежат в одной плоскости, а вершина общая.
Это доказательство демонстрирует, как геометрические свойства и алгебраические вычисления сочетаются для подтверждения равенства объемов.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!