
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1308 Атанасян — Подробные Ответы
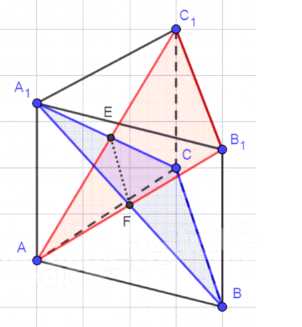
Плоскости AB₁C₁ и А₁ВС разбивают правильную треугольную призму ABCA₁B₁C₁ на четыре части. Найдите объёмы этих частей, если объём призмы равен V.
Объем призмы \(V\) делится сечениями \(AB_1C_1\) и \(A_1BC\) на четыре части. Сечения пересекаются по линии \(DE\), параллельной основанию.
1. Сечение \(A_1BC\) делит призму на пирамиду \(A_1ABC\) (\(V/3\)) и оставшуюся часть (\(2V/3\)).
2. Внутри \(A_1ABC\) сечение \(AED\) создает пирамиду \(C-AA_1DE\) (\(V/12\)) и многогранник \(ADECB\) (\(V/4\)).
3. В оставшейся части (\(2V/3\)) сечение \(DEC_1B_1\) образует пирамиду \(A_1DEC_1B_1\) (\(V/6\)) и многогранник \(EDBCC_1B_1\) (\(V/2\)).
Итоговые объемы: \(V_1 = \frac{V}{12}\), \(V_2 = \frac{V}{4}\), \(V_3 = \frac{V}{6}\), \(V_4 = \frac{V}{2}\).
Дано: правильная треугольная призма \(ABCA_1B_1C_1\) с объемом \(V\). Рассматриваются сечения \(AB_1C_1\) и \(A_1BC\). Требуется найти объемы частей, на которые эти сечения делят призму: \(V_1, V_2, V_3, V_4\).
Прямоугольники \(AA_1B_1B\) и \(AA_1C_1C\) имеют диагонали \(AB_1\) и \(A_1B\), \(AC_1\) и \(A_1C\), которые пересекаются в точках \(D\) и \(E\) соответственно. Точки \(D\) и \(E\) делят диагонали пополам, так как являются центрами симметрии прямоугольников. Отрезок \(DE\) — это линия пересечения сечений \(AB_1C_1\) и \(A_1BC\), и он параллелен основанию \(ABC\), являясь средней линией в треугольнике \(A_1BC\).
Пусть высота призмы \(AA_1 = h\). Сечение \(A_1BC\) делит призму на две пирамиды: \(A_1ABC\) и \(A_1BCC_1B_1\). Объем пирамиды \(A_1ABC\) равен \(V_{A_1ABC} = \frac{1}{3} \cdot S_{ABC} \cdot h = \frac{1}{3} \cdot \left(\frac{V}{h}\right) \cdot h = \frac{V}{3}\). Тогда объем второй части \(V_{A_1BCC_1B_1} = V — \frac{V}{3} = \frac{2V}{3}\).
Пирамида \(A_1ABC\) дополнительно делится сечением \(AED\) на две меньшие пирамиды: \(C-AA_1DE\) и \(ADECB\). Так как \(DE\) — средняя линия треугольника \(A_1BC\), то треугольник \(A_1DE\) подобен \(A_1BC\) с коэффициентом подобия \(k = \frac{1}{2}\). Площади подобных фигур относятся как квадрат коэффициента подобия: \(\frac{S_{A_1DE}}{S_{A_1BC}} = \left(\frac{1}{2}\right)^2 = \frac{1}{4}\). Следовательно, \(S_{A_1DE} = \frac{1}{4} S_{A_1BC}\), а площадь четырехугольника \(DECB\) составляет \(S_{DECB} = S_{A_1BC} — S_{A_1DE} = \frac{3}{4} S_{A_1BC}\).
Высоты пирамид \(C-AA_1DE\) и \(ADECB\) равны, так как они имеют общую вершину \(A\) и основание, лежащее в одной плоскости. Поэтому их объемы пропорциональны площадям оснований: \(V_{C-AA_1DE} = \frac{1}{4} V_{A_1ABC} = \frac{1}{4} \cdot \frac{V}{3} = \frac{V}{12}\), \(V_{ADECB} = \frac{3}{4} V_{A_1ABC} = \frac{3}{4} \cdot \frac{V}{3} = \frac{V}{4}\).
Теперь рассмотрим пирамиду \(A_1BCC_1B_1\), которая делится сечением \(DEC_1B_1\) на пирамиду \(A_1DEC_1B_1\) и многогранник \(EDBCC_1B_1\). Так как \(DE\) — средняя линия и в треугольнике \(AB_1C_1\), то аналогично \(S_{DEC_1B_1} = \frac{1}{4} S_{AB_1C_1}\). Объем \(V_{A_1DEC_1B_1} = \frac{1}{4} V_{A_1BCC_1B_1} = \frac{1}{4} \cdot \frac{2V}{3} = \frac{V}{6}\).
Наконец, объем многогранника \(EDBCC_1B_1\) равен разности: \(V_{EDBCC_1B_1} = V_{A_1BCC_1B_1} — V_{A_1DEC_1B_1} = \frac{2V}{3} — \frac{V}{6} = \frac{V}{2}\).
Итоговые объемы частей: \(V_1 = \frac{V}{12}\) (пирамида \(C-AA_1DE\)), \(V_2 = \frac{V}{4}\) (пирамида \(ADECB\)), \(V_3 = \frac{V}{6}\) (пирамида \(A_1DEC_1B_1\)), \(V_4 = \frac{V}{2}\) (многогранник \(EDBCC_1B_1\)).
Ответ: \(V_1 = \frac{V}{12}\), \(V_2 = \frac{V}{4}\), \(V_3 = \frac{V}{6}\), \(V_4 = \frac{V}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!