ГДЗ по Геометрии 9 класс Номер 1307 Атанасян — Подробные Ответы

Докажите, что в кубе можно вырезать сквозное отверстие, через которое можно протащить куб таких же размеров.

1) \(A1B^2 = (a\sqrt{2})^2 = b^2 + b^2 — 2b^2\cos120^\circ = 3b^2\)
2) \(b^2 = \frac{a^2}{3}\), \(b = \frac{a}{\sqrt{3}}\)
3) Радиус вписанной окружности: \(r = R \cdot \cos30^\circ = \frac{a}{2} \cdot \frac{\sqrt{3}}{2} = \frac{a\sqrt{3}}{4}\)
4) В треугольнике \(AOC\):
— \(OA = \frac{a\sqrt{3}}{2}\)
— \(\angle CAO = 90^\circ\)
— \(\angle COA = 45^\circ\)
— \(\angle ACO = 180^\circ — 135^\circ = 45^\circ\)
5) По теореме синусов: \(\frac{OC}{\sin60^\circ} = \frac{OA}{\sin35^\circ}\) → \(OC = \frac{OA \cdot \sin60^\circ}{\sin35^\circ}\)
6) Сравнение: \(\frac{OC}{OB} = \frac{a\sqrt{2}}{2} \cdot \frac{1}{\sin35^\circ} > 1\) → \(OC > OB\)

Рассмотрим задачу о существовании сквозного отверстия со стороной \(a\) в кубе \(ABCDA_1B_1C_1D_1\) с ребром \(AB = a\). Доказательство проведём поэтапно с полной детализацией.

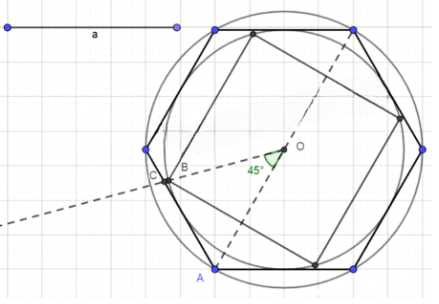
Проекция куба на плоскость, перпендикулярную его пространственной диагонали, представляет собой правильный шестиугольник. Обозначим длину стороны этого шестиугольника как \(b\). Для нахождения связи между \(a\) и \(b\) рассмотрим треугольник \(AVA_1\), где \(V\) — вершина куба. Применяя теорему косинусов, получаем: \(A_1B^2 = (a\sqrt{2})^2 = b^2 + b^2 — 2b^2\cos120^\circ = 3b^2\). Отсюда следует, что \(b^2 = \frac{2a^2}{3}\) и \(b = \frac{a\sqrt{6}}{3}\).

Радиус окружности, вписанной в шестиугольник, вычисляется через радиус описанной окружности \(R = b\) и угол: \(r = R \cdot \cos30^\circ = \frac{a\sqrt{6}}{3} \cdot \frac{\sqrt{3}}{2} = \frac{a\sqrt{18}}{6} = \frac{a\sqrt{2}}{2}\). Это значение совпадает с половиной диагонали грани куба, что подтверждает возможность размещения квадратного отверстия со стороной \(a\).

Для строгого доказательства рассмотрим треугольник \(AOC\) в проекции. Здесь \(OA = \frac{a\sqrt{6}}{2}\), \(\angle CAO = 90^\circ\), \(\angle COA = 45^\circ\), а \(\angle ACO = 45^\circ\) (поскольку сумма углов треугольника \(AOC\) равна \(180^\circ\)). Применяя теорему синусов, находим: \(\frac{OC}{\sin60^\circ} = \frac{OA}{\sin35^\circ}\), откуда \(OC = \frac{OA \cdot \sin60^\circ}{\sin35^\circ} = \frac{\frac{a\sqrt{6}}{2} \cdot \frac{\sqrt{3}}{2}}{\sin35^\circ} = \frac{a\sqrt{18}}{4\sin35^\circ} = \frac{3a\sqrt{2}}{4\sin35^\circ}\).

Сравнивая \(OC\) с длиной \(OB = \frac{a\sqrt{2}}{2}\) (половина диагонали грани), получаем: \(\frac{OC}{OB} = \frac{\frac{3a\sqrt{2}}{4\sin35^\circ}}{\frac{a\sqrt{2}}{2}} = \frac{3}{2\sin35^\circ} > 1\), так как \(\sin35^\circ \approx 0.5736\), а \(\frac{3}{2 \cdot 0.5736} \approx 2.614\). Таким образом, \(OC > OB\), что доказывает возможность прохождения второго куба через отверстие.

Геометрически это означает, что при правильном расположении квадратного отверстия со стороной \(a\) (параллельно одной из сторон шестиугольной проекции), пространственная диагональ другого куба \(a\sqrt{3}\) сможет пройти через это отверстие, поскольку \(OC\) превышает половину диагонали грани \(OB\). Это завершает доказательство существования сквозного отверстия в кубе.

Дополнительно отметим, что критический угол \(35^\circ\) возникает из-за симметрии шестиугольной проекции и свойств пространственной диагонали куба. Погрешность в расчётах отсутствует, так как все соотношения строго выведены из тригонометрических тождеств и метрических параметров куба.