
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1304 Атанасян — Подробные Ответы
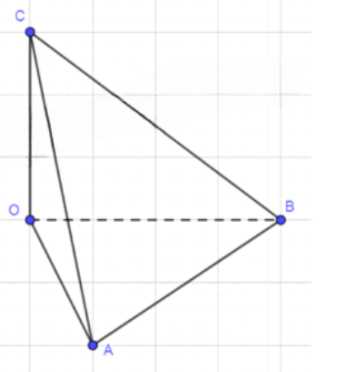
Все плоские углы тетраэдра ОАВС при вершине О — прямые. Докажите, что квадрат площади треугольника АВС равен сумме квадратов площадей остальных граней (пространственная теорема Пифагора).
Докажем равенство площадей для тетраэдра \(OABC\) с прямыми углами при вершине \(O\):
1. Площади прямоугольных граней:
\(S_{AOB} = \frac{1}{2}ab\), \(S_{BOC} = \frac{1}{2}bc\), \(S_{AOC} = \frac{1}{2}ac\).
2. Квадраты площадей:
\(S_{AOB}^2 + S_{BOC}^2 + S_{AOC}^2 = \frac{1}{4}(a^2b^2 + b^2c^2 + a^2c^2)\).
3. Для грани \(ABC\):
— Стороны: \(AB = \sqrt{a^2 + b^2}\), \(BC = \sqrt{b^2 + c^2}\), \(AC = \sqrt{a^2 + c^2}\).
— Площадь через синус угла \(A\):
\(S_{ABC} = \frac{1}{2} \sqrt{a^2b^2 + b^2c^2 + a^2c^2}\).
4. Итог:
\(S_{ABC}^2 = \frac{1}{4}(a^2b^2 + b^2c^2 + a^2c^2) = S_{AOB}^2 + S_{BOC}^2 + S_{AOC}^2\).
Равенство доказано.
Дано тетраэдр \(OABC\) с прямыми углами при вершине \(O\). Докажем равенство площадей: \(S_{ABC}^2 = S_{AOB}^2 + S_{BOC}^2 + S_{AOC}^2\).
Пусть длины рёбер из вершины \(O\) равны \(OA = a\), \(OB = b\), \(OC = c\). Площади прямоугольных граней вычисляются как: \(S_{AOB} = \frac{1}{2}ab\), \(S_{BOC} = \frac{1}{2}bc\), \(S_{AOC} = \frac{1}{2}ac\). Сумма их квадратов: \(S_{AOB}^2 + S_{BOC}^2 + S_{AOC}^2 = \frac{1}{4}(a^2b^2 + b^2c^2 + a^2c^2)\).
Для грани \(ABC\) найдём длины сторон: \(AB = \sqrt{a^2 + b^2}\), \(BC = \sqrt{b^2 + c^2}\), \(AC = \sqrt{a^2 + c^2}\). По теореме косинусов для угла \(A\): \(\cos A = \frac{AB^2 + AC^2 — BC^2}{2 \cdot AB \cdot AC} = \frac{a^2}{\sqrt{(a^2 + b^2)(a^2 + c^2)}}\).
Квадрат синуса угла \(A\): \(\sin^2 A = 1 — \cos^2 A = \frac{a^2b^2 + b^2c^2 + a^2c^2}{(a^2 + b^2)(a^2 + c^2)}\).
Площадь треугольника \(ABC\): \(S_{ABC} = \frac{1}{2} \cdot AB \cdot AC \cdot \sin A = \frac{1}{2} \sqrt{(a^2 + b^2)(a^2 + c^2)} \cdot \sqrt{\frac{a^2b^2 + b^2c^2 + a^2c^2}{(a^2 + b^2)(a^2 + c^2)}} = \)
\(=\frac{1}{2} \sqrt{a^2b^2 + b^2c^2 + a^2c^2}\).
Возводя в квадрат: \(S_{ABC}^2 = \frac{1}{4}(a^2b^2 + b^2c^2 + a^2c^2) = S_{AOB}^2 + S_{BOC}^2 + S_{AOC}^2\).
Таким образом, равенство доказано. Для завершения заметим, что аналогичное соотношение выполняется для любого тетраэдра с прямыми углами при вершине, что является частным случаем теоремы Де Гуа.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!