ГДЗ по Геометрии 9 класс Номер 1303 Атанасян — Подробные Ответы

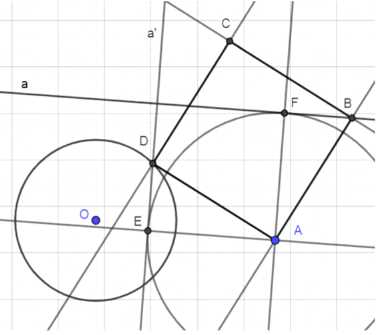
Даны прямая, окружность и точка А, не лежащая на них. Постройте квадрат ABCD так, чтобы вершина В лежала на данной прямой, а вершина D — на данной окружности.

Построение квадрата \(ABCD\):
1. Через точку \(A\) проводим перпендикуляр \(AF\) к прямой \(a\) и равный ему отрезок \(AE \perp AF\).
2. Строим прямую \(a’\) (поворот \(a\) на \(90^\circ\) вокруг \(A\)) через \(E\).
3. Точка \(D\) — пересечение \(a’\) и окружности \(O\).
4. Через \(A\) проводим перпендикуляр к \(AD\), точка \(B\) — пересечение с прямой \(a\).
5. Завершаем построение перпендикулярами \(DC \perp AD\) и \(BC \perp AB\), получая квадрат \(ABCD\).

Построение квадрата \(ABCD\) с заданными условиями \(B \in a\) и \(D \in O\) выполняется следующим образом. Через точку \(A\) проводим перпендикуляр \(AF\) к прямой \(a\) и перпендикуляр \(AE\) к прямой \(AF\), при этом длина отрезка \(AE\) равна длине отрезка \(AF\), то есть \(|AE| = |AF|\). Затем через точку \(E\) проводим перпендикуляр \(a’\) к прямой \(AE\), который является отображением прямой \(a\) при повороте на \(90^\circ\) вокруг точки \(A\). Точку \(D\) отмечаем на пересечении прямой \(a’\) и окружности \(O\). Далее через точку \(A\) проводим перпендикуляр к отрезку \(AD\) и отмечаем точку \(B\) на пересечении этого перпендикуляра с прямой \(a\). Завершаем построение проведением перпендикуляров \(DC \perp AD\) и \(BC \perp AB\), которые пересекаются в точке \(C\), формируя квадрат \(ABCD\).

Все шаги основаны на свойствах перпендикулярных прямых и поворота на \(90^\circ\), что гарантирует равенство сторон и углов квадрата. Построение использует только циркуль и линейку, следуя классическим методам геометрических построений.