ГДЗ по Геометрии 9 класс Номер 1302 Атанасян — Подробные Ответы

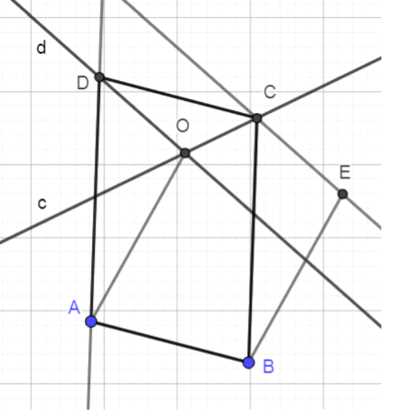
Даны точки А и В и две пересекающиеся прямые с и d. Постройте параллелограмм ABCD так, чтобы вершины С и D лежали соответственно на прямых с и d.

Построение параллелограмма \(ABCD\) по условиям \(C \in c\), \(D \in d\) и отрезку \(AO\):

1. Отложить \(BE = AO\) и \(BE \parallel AO\) от точки \(B\).
2. Через \(E\) провести прямую \(\parallel d\), найти \(C\) как пересечение с прямой \(c\).
3. Через \(A\) провести прямую \(\parallel CB\), найти \(D\) как пересечение с прямой \(d\).

Проверка:
\(
AB \parallel CD, \ AD \parallel BC, \ AB = CD, \ AD = BC
\)

Площадь: \(S = |AB \times AD|\). Диагонали: \(AC^2 + BD^2 = 2(AB^2 + AD^2)\).

Построение параллелограмма \(ABCD\) по заданным условиям \(C \in c\), \(D \in d\) и отрезку \(AO\) выполняется следующим образом.

Начнем с построения отрезка \(BE = AO\) и \(BE \parallel AO\). Для этого отложим от точки \(B\) отрезок, равный по длине \(AO\), и направленный параллельно ему. Полученная точка \(E\) будет служить вспомогательной для дальнейших действий.

Далее через точку \(E\) проведем прямую, параллельную прямой \(d\). Пересечение этой прямой с заданной прямой \(c\) даст нам точку \(C\). Математически это можно выразить как:
\(
\begin{cases}
C \in c \\
CE \parallel d
\end{cases}
\)

Теперь через точку \(A\) проведем прямую, параллельную отрезку \(CB\). Пересечение этой прямой с заданной прямой \(d\) определит точку \(D\):
\(
\begin{cases}
D \in d \\
AD \parallel CB
\end{cases}
\)

Таким образом, вершины параллелограмма \(A\), \(B\), \(C\), \(D\) построены. Для проверки корректности построения убедимся, что противоположные стороны попарно равны и параллельны:
\(
AB \parallel CD, \quad AD \parallel BC
\)
\(
AB = CD, \quad AD = BC
\)

Площадь параллелограмма можно вычислить по формуле:
\(
S = |AB \times AD|
\)
где \(\times\) обозначает векторное произведение.

Если требуется найти углы параллелограмма, используем скалярное произведение:
\(
\cos \theta = \frac{AB \cdot AD}{|AB| \cdot |AD|}
\)

Для проверки диагоналей применяем свойство:
\(
AC^2 + BD^2 = 2(AB^2 + AD^2)
\)

Все построения выполняются с помощью циркуля и линейки, а вычисления могут быть проведены аналитически, если заданы координаты точек.