ГДЗ по Геометрии 9 класс Номер 1301 Атанасян — Подробные Ответы

Постройте трапецию, стороны которой соответственно равны данным отрезкам.

Построение трапеции \(ABCD\) по сторонам \(a\), \(b\), \(c\), \(d\):
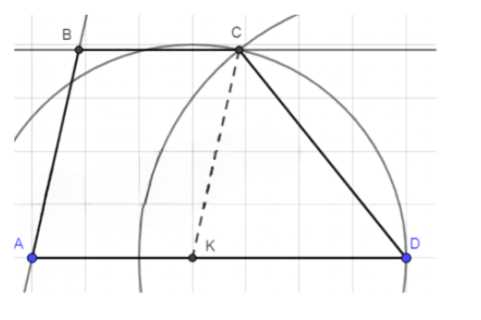
1. Отложим отрезок \(AD = a\), отметим точку \(K\) так, что \(AK = b\).
2. Построим окружности \((K; c)\) и \((D; d)\), их пересечение — точка \(C\).
3. Через \(A\) проведём прямую \(\parallel CK\), через \(C\) — прямую \(\parallel AD\). Их пересечение — точка \(B\).

Проверка:
— \(AD = a\), \(AB \parallel CD\) (по построению),
— \(CK = c\) (радиус), \(CD = d\) (радиус).

Если условия выполнены, трапеция построена верно.

Построение трапеции \(ABCD\) по заданным сторонам \(a\), \(b\), \(c\) и \(d\) выполняется следующим образом. Начнем с построения отрезка \(AD = a\). На этом отрезке отложим точку \(K\) так, чтобы \(AK = b\). Теперь построим две окружности: первую с центром в точке \(K\) и радиусом \(c\), вторую с центром в точке \(D\) и радиусом \(d\). Точка пересечения этих окружностей будет точкой \(C\).

Далее проведем через точку \(A\) прямую, параллельную отрезку \(CK\), и через точку \(C\) прямую, параллельную отрезку \(AD\). Точка пересечения этих двух прямых будет точкой \(B\). Таким образом, мы получим трапецию \(ABCD\) с основаниями \(AD = a\) и \(BC\), боковыми сторонами \(AB\) и \(CD = d\), а также отрезком \(CK = c\).

Для проверки корректности построения убедимся, что выполнены следующие условия: \(AB \parallel CD\) (по определению трапеции), \(AD = a\), \(AK = b\), \(CK = c\) и \(CD = d\). Если все условия соблюдены, построение можно считать верным.

Математически это можно выразить следующим образом: для точек \(A(x_1, y_1)\), \(D(x_2, y_2)\), \(K(x_3, y_3)\) и \(C(x_4, y_4)\) координаты вычисляются исходя из заданных длин. Например, положение точки \(K\) определяется как \(K = A + \frac{b}{a} \cdot (D — A)\). Координаты точки \(C\) находятся как решение системы уравнений окружностей: \((x — x_3)^2 + (y — y_3)^2 = c^2\) и \((x — x_2)^2 + (y — y_2)^2 = d^2\).

После нахождения точки \(C\) прямые \(AB\) и \(CB\) строятся с учетом условий параллельности: направляющий вектор прямой \(AB\) совпадает с направляющим вектором \(CK\), а направляющий вектор прямой \(CB\) совпадает с направляющим вектором \(AD\). Точка \(B\) находится как пересечение этих прямых.

Таким образом, трапеция \(ABCD\) полностью определена. Для проверки можно вычислить длины всех сторон и убедиться, что они соответствуют заданным значениям \(a\), \(b\), \(c\) и \(d\). Если длины совпадают, построение выполнено верно.