
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1300 Атанасян — Подробные Ответы
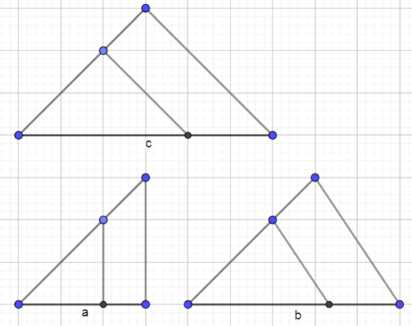
Постройте треугольник по трём медианам.
Построение треугольника \( \triangle ABC \) по медианам \( a \), \( b \), \( c \):
1. Разделим медианы на части \( \frac{2}{3} \) и \( \frac{1}{3} \).
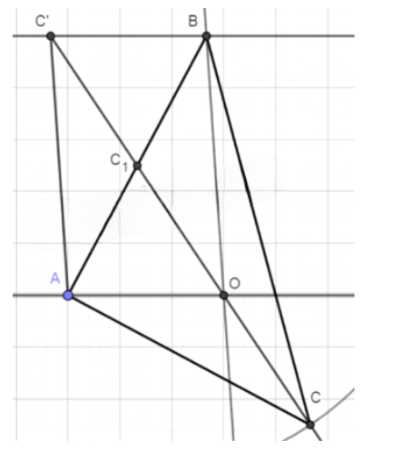
2. Строим \( \triangle AOC’ \) со сторонами \( AO = \frac{2}{3}a \), \( OC’ = \frac{2}{3}b \), \( AC’ = \frac{2}{3}c \).
3. Через \( C’ \) проводим прямую \( \parallel AO \), через \( O \) — прямую \( \parallel C’A \). Их пересечение даёт точку \( B \).
4. Находим середину \( AB \) — точку \( C_1 \).
5. На луче \( C_1O \) откладываем \( C_1C = c \).
Полученные точки \( A \), \( B \), \( C \) образуют искомый треугольник.
Построение треугольника \( \triangle ABC \) по заданным медианам \( a \), \( b \) и \( c \) выполняется следующим образом.
Медианы делятся на три части, так как точка пересечения медиан делит их в отношении \( 2:1 \). Таким образом, каждая медиана состоит из двух отрезков: \( \frac{2}{3} \) и \( \frac{1}{3} \) от её длины.
Сначала строим треугольник \( \triangle AOC’ \), где:
\( AO = \frac{2}{3}a \)
\( OC’ = \frac{2}{3}b \)
\( AC’ = \frac{2}{3}c \)
Затем через точку \( C’ \) проводим прямую, параллельную \( AO \), а через точку \( O \) — прямую, параллельную \( C’A \). Точка пересечения этих прямых будет вершиной \( B \).
Далее находим середину отрезка \( AB \) — точку \( C_1 \). На продолжении луча \( C_1O \) откладываем отрезок \( C_1C = c \), где \( c \) — заданная медиана.
Теперь соединяем точки \( A \), \( B \) и \( C \), получая искомый треугольник \( \triangle ABC \).
Для проверки корректности построения можно убедиться, что медианы \( AA_1 \), \( BB_1 \) и \( CC_1 \) действительно равны \( a \), \( b \) и \( c \) соответственно.
Если требуется дополнительное обоснование, можно использовать свойство медиан:
\( m_a = \frac{1}{2} \sqrt{2b^2 + 2c^2 — a^2} \)
\( m_b = \frac{1}{2} \sqrt{2a^2 + 2c^2 — b^2} \)
\( m_c = \frac{1}{2} \sqrt{2a^2 + 2b^2 — c^2} \)
Эти формулы позволяют проверить, что построенный треугольник удовлетворяет заданным условиям.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!