
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1299 Атанасян — Подробные Ответы
Даны две пересекающиеся окружности. Постройте отрезок, концы которого лежат соответственно на данных окружностях, а его середина совпадает с одной из точек пересечения данных окружностей.
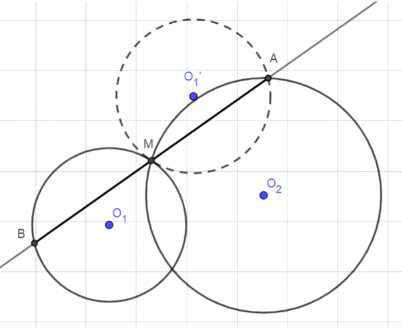
Дано две окружности \( \omega_1 \) и \( \omega_2 \) с центрами \( O_1 \) и \( O_2 \), а также точка \( M \). Строим окружность \( \omega_1′ \), симметричную \( \omega_1 \) относительно \( M \): её центр \( O_1′ = 2M — O_1 \), радиус тот же. Находим пересечение \( \omega_1′ \) и \( \omega_2 \) — это точка \( A \). Тогда \( B = 2M — A \) лежит на \( \omega_1 \), а отрезок \( AB \) имеет середину \( M \). Если пересечений нет, решения нет.
Дано две окружности \( \omega_1 \) и \( \omega_2 \) с центрами \( O_1 \) и \( O_2 \) соответственно, а также точка \( M \). Требуется построить отрезок, концы которого лежат на \( \omega_1 \) и \( \omega_2 \), а точка \( M \) является его серединой.
Построение выполняется следующим образом. Сначала строим окружность \( \omega_1′ \), симметричную \( \omega_1 \) относительно точки \( M \). Это означает, что для любой точки \( A \) на \( \omega_1 \) существует точка \( A’ \) на \( \omega_1′ \), такая что \( M \) — середина отрезка \( AA’ \). Математически это можно выразить как \( A’ = 2M — A \).
Далее находим точку пересечения \( \omega_1′ \) и \( \omega_2 \). Пусть это точка \( A \). Поскольку \( A \) лежит на \( \omega_1′ \), то существует точка \( B \) на \( \omega_1 \), для которой \( M \) — середина отрезка \( AB \). Таким образом, \( B = 2M — A \).
Проводим прямую \( AM \). Точка \( B \) должна лежать на пересечении этой прямой с \( \omega_1 \), так как \( B \) симметрична \( A \) относительно \( M \). Отрезок \( AB \) является искомым, так как \( M \) — его середина, \( A \) лежит на \( \omega_2 \), а \( B \) — на \( \omega_1 \).
Обоснование корректности построения: поскольку \( A \) лежит на \( \omega_1′ \), то \( B = 2M — A \) лежит на \( \omega_1 \), так как \( \omega_1′ \) — образ \( \omega_1 \) при симметрии относительно \( M \). Точка \( A \) также лежит на \( \omega_2 \) по построению. Таким образом, \( AB \) — отрезок с концами на \( \omega_1 \) и \( \omega_2 \), а \( M \) — его середина.
Если окружности \( \omega_1′ \) и \( \omega_2 \) не пересекаются, задача не имеет решения. Если они касаются, существует ровно одно решение. Если пересекаются в двух точках, то возможны два различных отрезка, удовлетворяющих условию.
Дополнительно можно рассмотреть аналитическое решение. Пусть \( O_1 = (x_1, y_1) \), \( O_2 = (x_2, y_2) \), \( M = (x_m, y_m) \), радиусы окружностей \( r_1 \) и \( r_2 \). Тогда уравнение \( \omega_1′ \) имеет вид \( (x — (2x_m — x_1))^2 + (y — (2y_m — y_1))^2 = r_1^2 \). Пересечение с \( \omega_2 \) даёт систему уравнений, решение которой приводит к координатам точки \( A \), а затем и \( B \).
Таким образом, построение завершено, и отрезок \( AB \) удовлетворяет всем условиям задачи.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!