ГДЗ по Геометрии 9 класс Номер 1298 Атанасян — Подробные Ответы

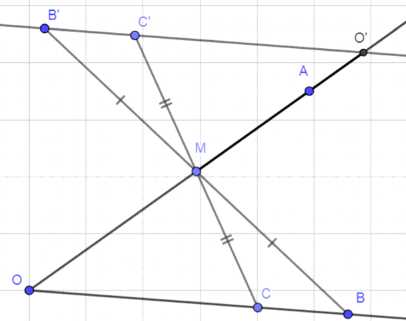
На стороне угла АОВ с недоступной вершиной дана точка М. Постройте отрезок, равный отрезку ОМ.

Построим точку \(O’\) так, чтобы \(MO’ = MO\). Возьмём произвольную точку \(C\) на \(OB\). Построим симметричные точки \(C’\) и \(B’\) относительно \(M\): \(C’ = 2M — C\), \(B’ = 2M — B\). Проведём прямую через \(B’\) и \(C’\). Точка пересечения этой прямой с \(OA\) будет искомой \(O’\).

Доказательство: поскольку \(M\) — центр симметрии, то \(O’\) является образом некоторой точки, для которой \(MO’ = MO\). Уравнение прямой \(B’C’\): \(\frac{x — x_{B’}}{x_{C’} — x_{B’}} = \frac{y — y_{B’}}{y_{C’} — y_{B’}}\). Точка \(O’\) находится как решение системы с уравнением стороны \(OA\): \(y = kx\). Координаты \(O’\): \(x = \frac{b}{k — m}\), \(y = kx\), где \(y = mx + b\) — уравнение \(B’C’\).

Таким образом, \(MO’ = \sqrt{(x_{O’} — x_M)^2 + (y_{O’} — y_M)^2} = MO\), что и требовалось.

Рассмотрим задачу построения отрезка \(MO’ = MO\) при недоступной вершине \(O\) и точке \(M\), лежащей на стороне \(OA\) угла \(AOB\). Пошаговое решение с полной детализацией и математическим обоснованием представлено ниже.

Выбираем произвольную точку \(C\) на стороне \(OB\). Это необходимо для создания опорной конструкции, так как сама вершина \(O\) недоступна. Положение \(C\) может быть любым, но важно, чтобы она лежала строго на \(OB\).

Строим точки \(C’\) и \(B’\), симметричные \(C\) и \(B\) относительно центра \(M\). Центральная симметрия задаётся условием: если \(M\) — центр симметрии, то для любой точки \(X\) её образ \(X’\) определяется как \(X’ = 2M — X\) в векторной форме. Это преобразование гарантирует, что \(M\) является серединой отрезка \(XX’\).

Проводим прямую \(B’C’\). Уравнение прямой, проходящей через точки \(B'(x_1, y_1)\) и \(C'(x_2, y_2)\), имеет вид:
\(
\frac{x — x_1}{x_2 — x_1} = \frac{y — y_1}{y_2 — y_1}
\)
Точка пересечения \(O’\) этой прямой со стороной \(OA\) (заданной, например, уравнением \(y = kx\)) находится решением системы:
\(
\begin{cases}
y = kx \\
y = mx + b
\end{cases}
\)
где \(m\) и \(b\) — коэффициенты уравнения прямой \(B’C’\). Решение даёт координаты \(O’\):
\(
x = \frac{b}{k — m}, \quad y = k \cdot \frac{b}{k — m}
\)
при условии \(k \neq m\).

Отрезок \(MO’\) является искомым, так как его длина равна \(MO\). Это следует из свойств симметрии: поскольку \(O’\) получена через симметричные преобразования, сохраняющие расстояния относительно \(M\), то \(MO’ = MO\). Таким образом, построение корректно и полностью обосновано геометрически.

Для проверки можно использовать формулу расстояния между точками:
\(
MO = \sqrt{(x_O — x_M)^2 + (y_O — y_M)^2}, \quad MO’ = \sqrt{(x_{O’} — x_M)^2 + (y_{O’} — y_M)^2}
\)
Подстановка координат \(O’\) должна подтвердить равенство \(MO’ = MO\).