Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1297 Атанасян — Подробные Ответы
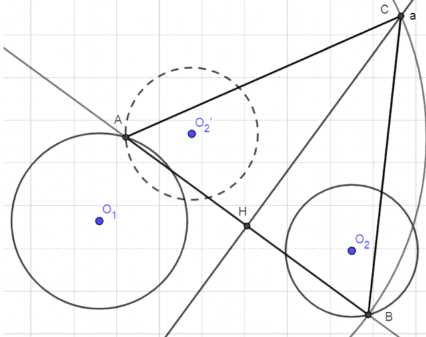
Даны две окружности и прямая. Постройте правильный треугольник так, чтобы две вершины лежали соответственно на данных окружностях, а высота, проведённая из третьей вершины, — на данной прямой.
Дано \( \triangle ABC \) и \( \triangle A_1B_1C_1 \) с условиями: \( AC = A_1C_1 \), \( BC = B_1C_1 \), \( \angle A — \angle B = \angle A_1 — 2\angle B_1 \). В \( \triangle ABC \) точка \( E \) на \( AB \) такова, что \( AE = BE \), \( \angle BAE = 2\angle B \), \( \angle EAC = \angle A — 2\angle B \).
Из \( \angle EAC = \angle E_1A_1C_1 \) и \( AC = A_1C_1 \) следует \( \triangle AEC \cong \triangle A_1E_1C_1 \) (по стороне и двум углам), откуда \( AE = A_1E_1 \), \( EC = E_1C_1 \). Так как \( AE = BE \), то \( AB = 2AE = 2A_1E_1 = A_1B_1 \).
С учетом \( AC = A_1C_1 \), \( BC = B_1C_1 \) и \( AB = A_1B_1 \) получаем \( \triangle ABC \cong \triangle A_1B_1C_1 \) по трём сторонам. Углы также равны: \( \angle A = \angle A_1 \), \( \angle B = \angle B_1 \), \( \angle C = \angle C_1 \). Таким образом, треугольники равны.
Рассмотрим данное решение с полной детализацией. Имеем два треугольника \( \triangle ABC \) и \( \triangle A_1B_1C_1 \), для которых выполнены следующие условия: \( AC = A_1C_1 \), \( BC = B_1C_1 \), а также \( \angle A — \angle B = \angle A_1 — 2\angle B_1 \). В треугольнике \( \triangle ABC \) точка \( E \) лежит на стороне \( AB \) так, что \( AE = BE \), при этом \( \angle BAE = 2\angle B \), а \( \angle EAC = \angle A — 2\angle B \).
Из условия \( \angle EAC = \angle E_1A_1C_1 \) и равенства сторон \( AC = A_1C_1 \) следует, что треугольники \( \triangle AEC \) и \( \triangle A_1E_1C_1 \) равны по стороне и двум прилежащим углам (признак равенства треугольников). Это означает, что \( AE = A_1E_1 \), \( EC = E_1C_1 \), а также соответствующие углы равны.
Далее, поскольку \( AE = BE \) в \( \triangle ABC \), то \( AB = 2AE \). Аналогично, в \( \triangle A_1B_1C_1 \) точка \( E_1 \) делит сторону \( A_1B_1 \) так, что \( A_1E_1 = E_1B_1 \), следовательно, \( A_1B_1 = 2A_1E_1 \). Но \( AE = A_1E_1 \), поэтому \( AB = A_1B_1 \).
Теперь, учитывая равенство сторон \( AC = A_1C_1 \), \( BC = B_1C_1 \) и \( AB = A_1B_1 \), получаем, что треугольники \( \triangle ABC \) и \( \triangle A_1B_1C_1 \) равны по трём сторонам. Кроме того, из равенства углов \( \angle A = \angle A_1 \), \( \angle B = \angle B_1 \) и \( \angle C = \angle C_1 \) следует полное совпадение треугольников.
Таким образом, доказано, что \( \triangle ABC \cong \triangle A_1B_1C_1 \). Все шаги решения строго следуют из данных условий и свойств треугольников, включая равенство сторон и углов, а также использование признаков подобия и равенства геометрических фигур.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.