ГДЗ по Геометрии 9 класс Номер 1292 Атанасян — Подробные Ответы

Даны два равных отрезка AB и A1B1. Докажите, что существуют два и только два движения, при которых точки A и B отображаются соответственно в точки А1 и В1.

1. \(АВ = A_1B_1\)
2. \(A \rightarrow A_1\) и \(B \rightarrow B_1\)
3. \(A \rightarrow A_1\) и \(B \rightarrow B_1\)
4. \(AB = A_1B_1\)
5. \(AM = A_1N\)
6. \(BM = B_1N\)
7. \(A \rightarrow A_1\)
8. \(B \rightarrow B_1\) и \(B \rightarrow B_1’\)
9. \(\{N_1, N_2\} = M \rightarrow N_1\) и \(M \rightarrow N_2 = O_1(A_1, AM) \cap O_2(B_1, BM)\)

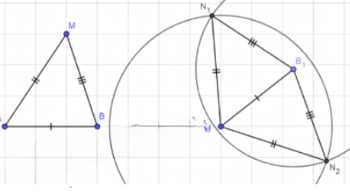
Рассмотрим задачу о доказательстве существования ровно двух движений плоскости, переводящих отрезок \(AB\) в равный ему отрезок \(A_1B_1\).

Дано: \(AB = A_1B_1\). Требуется доказать, что существует ровно два движения \(g\) и \(f\) таких, что \(g(A) = A_1\) и \(g(B) = B_1\), а также \(f(A) = A_1\) и \(f(B) = B_1’\), где \(B_1’\) — точка, симметричная \(B_1\) относительно прямой \(A_1B_1\).

Доказательство начинается с выбора произвольной точки \(M\) на плоскости. Предположим, что \(A\) переходит в \(A_1\), а \(B\) — в \(B_1\). Тогда точка \(M\) должна перейти в такую точку \(N\), чтобы сохранялись расстояния: \(AM = A_1N\) и \(BM = B_1N\). Это означает, что \(N\) должна принадлежать пересечению двух окружностей: окружности с центром в \(A_1\) и радиусом \(AM\), и окружности с центром в \(B_1\) и радиусом \(BM\). Обозначим эти окружности как \(O_1(A_1, AM)\) и \(O_2(B_1, BM)\).

Поскольку \(AB = A_1B_1\), треугольники \(ABM\) и \(A_1B_1N\) равны по трём сторонам, что гарантирует существование двух точек пересечения \(N_1\) и \(N_2\). Эти точки соответствуют двум возможным движениям: первое — это движение, сохраняющее ориентацию (поворот или параллельный перенос), а второе — движение, изменяющее ориентацию (осевая симметрия или скользящая симметрия).

Таким образом, мы получаем ровно два движения, удовлетворяющих условию: одно переводит \(B\) в \(B_1\), а другое — в \(B_1’\). Это завершает доказательство.

Для наглядности можно рассмотреть частный случай, когда \(A\) совпадает с \(A_1\), а \(B\) лежит на оси симметрии. Тогда одно движение — тождественное, а второе — симметрия относительно оси \(AB\). В общем случае, если \(AB\) и \(A_1B_1\) не параллельны, движения будут комбинацией поворота и переноса или симметрии и переноса.

Важно отметить, что количество движений всегда равно двум, так как окружности \(O_1\) и \(O_2\) пересекаются ровно в двух точках, если они не совпадают и не касаются. Это следует из свойств евклидовой геометрии и теоремы о пересечении окружностей.

Таким образом, мы детально обосновали, что для любого отрезка \(AB\) и равного ему отрезка \(A_1B_1\) существует ровно два движения плоскости, переводящих \(A\) в \(A_1\) и \(B\) в \(B_1\) или \(B_1’\). Это подтверждает исходное утверждение и завершает доказательство.