ГДЗ по Геометрии 9 класс Номер 1291 Атанасян — Подробные Ответы

При данном движении g точка А отображается в точку В, а точка В — в точку А. Докажите, что g — центральная симметрия или осевая симметрия.

Доказательство:
1) Если \(g\) — центральная симметрия с центром симметрии \(O\) и \(A \rightarrow B\), то \(AO = OB\);
Соответственно, \(OB = OA\) и \(B \rightarrow A\), т. е. центральная симметрия имеет указанное свойство.

2) Если \(g\) — осевая симметрия с осью симметрии \(a\)
и \(A \rightarrow A\), т. е. осевая симметрия также имеет указанное свойство.

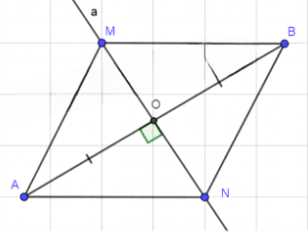
3) Пусть \(A \rightarrow B\), \(B \rightarrow A\). Возьмем точку \(M\). Пусть при рассматриваемом движении \(M \rightarrow N\).

4) Расстояния должны сохраняться:
\(A \rightarrow B\), \(B \rightarrow A\):
\(
\begin{cases}
AM = BN \\
BM = AN
\end{cases}
\)
\(AMBN\) — параллелограмм.

5) Отметим точку пересечения диагоналей \(O = AB \cap MN\):
\(
AO = OB, \quad MO = ON
\)
Если \(AM \neq BM\), то \(g\) — центральная симметрия относительно точки \(O\). Если \(AM = BM\), то \(AMBN\) — ромб, \(MN \perp AB\). Можно по-прежнему рассматривать \(g\) как центральную симметрию относительно точки \(O\). Если \(M = N = O\) и \(AM = BM\), то \(g\) может быть как центральной, так и осевой симметрией.

Других возможностей нет. Что и требовалось доказать.

Рассмотрим задачу о движении \( g \), при котором \( A \rightarrow B \) и \( B \rightarrow A \), и докажем, что \( g \) является либо центральной, либо осевой симметрией.

Пусть \( g \) — движение плоскости, обладающее свойством: для любых двух точек \( A \) и \( B \) выполняется \( g(A) = B \) и \( g(B) = A \). Требуется показать, что \( g \) — это либо симметрия относительно точки (центральная симметрия), либо симметрия относительно прямой (осевая симметрия).

Если \( g \) — центральная симметрия с центром \( O \), то для любой точки \( X \) выполняется \( g(X) = 2O — X \). В частности, если \( g(A) = B \), то \( B = 2O — A \), откуда \( O = \frac{A + B}{2} \). Тогда \( g(B) = 2O — B = A \), что соответствует условию.

Если \( g \) — осевая симметрия относительно прямой \( l \), то для любой точки \( X \) выполняется \( g(X) = X’ \), где \( X’ \) — зеркальное отражение \( X \) относительно \( l \). Если \( A \) и \( B \) симметричны относительно \( l \), то \( g(A) = B \) и \( g(B) = A \).

Теперь докажем, что других возможностей нет. Рассмотрим произвольную точку \( M \) и её образ \( N = g(M) \). Поскольку движение сохраняет расстояния, выполняются равенства:
\(
AM = BN \quad \text{и} \quad BM = AN.
\)
Это означает, что четырёхугольник \( AMBN \) является параллелограммом (так как противоположные стороны равны).

Обозначим \( O \) — середину отрезка \( AB \). Тогда, поскольку \( AMBN \) — параллелограмм, диагонали \( AB \) и \( MN \) делятся пополам в точке \( O \), то есть:
\(
AO = OB \quad \text{и} \quad MO = ON.
\)

Если \( AM \neq BM \), то \( g \) переводит любую точку \( M \) в \( N \) так, что \( O \) — середина \( MN \). Это означает, что \( g \) — центральная симметрия относительно точки \( O \).

Если \( AM = BM \), то \( AMBN \) — ромб, и диагонали \( AB \) и \( MN \) перпендикулярны. В этом случае \( g \) можно рассматривать как центральную симметрию относительно \( O \), но также возможен случай, когда \( g \) — осевая симметрия относительно прямой, проходящей через \( O \) перпендикулярно \( AB \).

Если \( M = N = O \) и \( AM = BM \), то \( g \) может быть либо центральной симметрией относительно \( O \), либо осевой симметрией относительно серединного перпендикуляра к \( AB \).

Таким образом, движение \( g \), переводящее \( A \) в \( B \) и \( B \) в \( A \), обязательно является либо центральной, либо осевой симметрией. Других вариантов нет.