ГДЗ по Геометрии 9 класс Номер 1290 Атанасян — Подробные Ответы

Постройте границу круга, площадь которого равна:
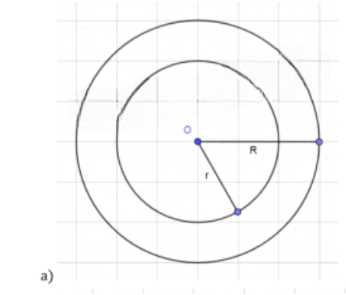
а) площади кольца между двумя данными концентрическими окружностями;
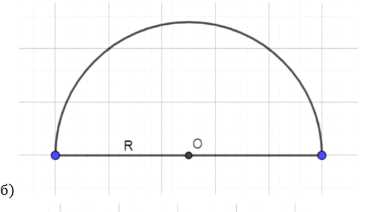
б) площади данного полукруга;
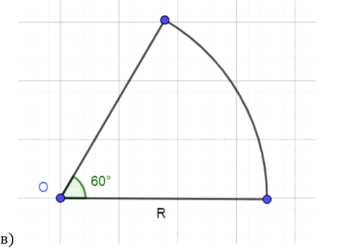
в) площади данного кругового сектора, ограниченного дугой в 60°.

Построение круга с площадью, равной заданным фигурам, выполняется следующим образом:

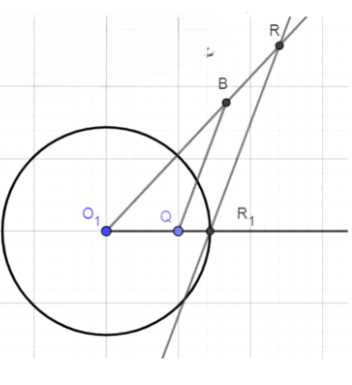
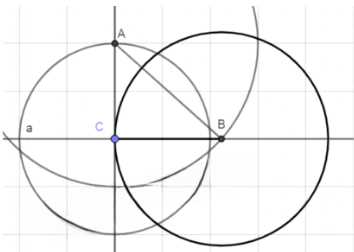
а) Для кольца между двумя концентрическими окружностями: площадь кольца равна разности площадей двух кругов \((S = \pi(R^2 — r^2))\). Чтобы построить круг с такой же площадью, радиус нового круга должен быть \((\sqrt{R^2 — r^2})\). Это соответствует теореме Пифагора. Строим перпендикуляр к прямой в точке C, отмечаем точку A на пересечении с окружностью \((C; r)\), затем строим окружность \((A; R)\) и находим точку B на пересечении с прямой. Искомый круг будет иметь центр в B и радиус BC.

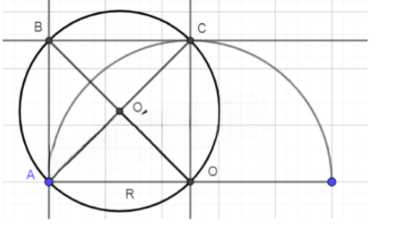
б) Для полукруга: площадь полукруга \((\frac{\pi R^2}{2})\) должна быть равна площади нового круга \((\pi r^2)\). Отсюда радиус нового круга \((r = \frac{R}{\sqrt{2}})\). Это половина диагонали квадрата со стороной R. Строим перпендикуляр к отрезку OA через точку O, находим точку C на пересечении с полуокружностью, затем строим перпендикуляры через точки A и C, отмечаем точку B на их пересечении. Центр искомого круга — точка пересечения диагоналей квадрата ABCO.

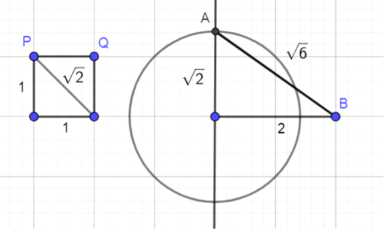
в) Для кругового сектора с дугой 60°: площадь сектора \((\frac{\pi R^2}{6})\) должна быть равна площади нового круга \((\pi r^2)\). Радиус нового круга \((r = \frac{R}{\sqrt{6}})\). Строим квадрат со стороной PQ (единичный отрезок), его диагональ \((\sqrt{2})\). Затем строим прямоугольный треугольник с катетами 2 и \((\sqrt{2})\), гипотенуза которого \((\sqrt{6})\). На сторонах угла откладываем отрезки, строим параллельную прямую и находим радиус нового круга.

Рассмотрим полное решение задачи о построении круга с площадью, равной площади заданных фигур, с детализацией каждого шага и математическими выкладками.

а) Кольцо между двумя концентрическими окружностями
Площадь кольца определяется разностью площадей внешнего и внутреннего кругов: \(S_{\text{кольца}} = \pi(R^2 — r^2)\). Чтобы построить круг с такой же площадью, приравняем её к площади нового круга: \(\pi(R^2 — r^2) = \pi r_{\text{нов}}^2\). Отсюда радиус нового круга: \(r_{\text{нов}} = \sqrt{R^2 — r^2}\).

Геометрическое построение:
1. Проводим прямую и отмечаем центр \(O\).
2. Строим окружность с радиусом \(r\) (внутренний радиус кольца).
3. На этой окружности выбираем точку \(A\) и проводим перпендикуляр к прямой через \(O\).
4. Строим окружность с центром в \(A\) и радиусом \(R\) (внешний радиус кольца), находим точку пересечения \(B\) с перпендикуляром.
5. Отрезок \(OB\) будет искомым радиусом \(r_{\text{нов}}\).

б) Полукруг
Площадь полукруга: \(S_{\text{полукр}} = \frac{\pi R^2}{2}\). Приравниваем к площади нового круга: \(\frac{\pi R^2}{2} = \pi r_{\text{нов}}^2\). Радиус нового круга: \(r_{\text{нов}} = \frac{R}{\sqrt{2}}\).

Геометрическое построение:
1. Строим диаметр \(AB\) и полуокружность с центром \(O\).
2. Проводим перпендикуляр к \(AB\) через точку \(O\), отмечаем точку \(C\) на пересечении с полуокружностью.
3. Строим квадрат \(AOCD\) со стороной \(R\).
4. Диагональ \(AD\) этого квадрата равна \(R\sqrt{2}\), а половина диагонали \( \frac{R}{\sqrt{2}} \) — искомый радиус.

в) Круговой сектор с углом 60°
Площадь сектора: \(S_{\text{сект}} = \frac{\pi R^2}{6}\). Приравниваем к площади нового круга: \(\frac{\pi R^2}{6} = \pi r_{\text{нов}}^2\). Радиус нового круга: \(r_{\text{нов}} = \frac{R}{\sqrt{6}}\).

Геометрическое построение:
1. Строим окружность с радиусом \(R\) и отмечаем центральный угол 60°.
2. На сторонах угла откладываем отрезки длиной \(R\) и \(1\) (единичный отрезок).
3. Строим прямоугольный треугольник с катетами \(2\) и \(\sqrt{2}\) (из предыдущего пункта).
4. Гипотенуза этого треугольника равна \(\sqrt{6}\), а отношение \(\frac{R}{\sqrt{6}}\) даёт искомый радиус.

Все построения основаны на классических методах геометрии с использованием циркуля и линейки, а также алгебраических соотношений между площадями и радиусами.