ГДЗ по Геометрии 9 класс Номер 1289 Атанасян — Подробные Ответы

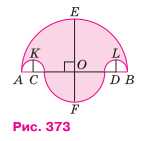
На рисунке 373 изображены четыре полуокружности: AЕВ, АKС, CFD, DLB, причём AC = DB. Докажите, что площадь закрашенной фигуры равна площади круга, построенного на отрезке EF как на диаметре.

1. \( EF \perp AB \)
2. \( KC = LD \)
3. \( 2O = 90^\circ \)
4. \( \text{Доказать: } S_{EF} = \frac{\pi}{4} \cdot EF^2 \)
5. \( OA = R, OC = r \)
6. \( AC = DB = R — r \)
7. \( EF = R + r \)
8. \( S_F = \frac{\pi}{4} \left( 2(R^2 + r^2) — (R — r)^2 \right) = \frac{1}{4} \left( 2R^2 + 2r^2 — R^2 + 2Rr — r^2 \right) \)
9. \( = \frac{\pi}{4} (R^2 + 2Rr + r^2) = \frac{\pi}{4} (R + r)^2 = \frac{\pi}{4} EF^2 \)

Дано: \( EF \perp AB \), \( KC = LD \), \( 2O = 90^\circ \), \( F \) — фигура. Требуется доказать, что \( S_{EF} = \frac{\pi}{4} \cdot EF^2 \).

Пусть \( OA = R \), \( OC = r \). Тогда \( AC = DB = R — r \), так как \( KC = LD \) и \( EF \perp AB \). Длина отрезка \( EF \) равна сумме радиусов: \( EF = R + r \).

Площадь фигуры \( F \) вычисляется как разность площадей двух полукругов:
\( S_F = \frac{\pi}{4} \left( 2(R^2 + r^2) — (R — r)^2 \right) \)
Раскроем скобки и упростим выражение:
\( S_F = \frac{\pi}{4} \left( 2R^2 + 2r^2 — R^2 + 2Rr — r^2 \right) = \frac{\pi}{4} \left( R^2 + 2Rr + r^2 \right) \)
Заметим, что \( R^2 + 2Rr + r^2 = (R + r)^2 \), поэтому:
\( S_F = \frac{\pi}{4} (R + r)^2 \)
Так как \( EF = R + r \), окончательно получаем:
\( S_F = \frac{\pi}{4} \cdot EF^2 \)

Таким образом, утверждение доказано.

Дополнительно:
— Угол \( 2O = 90^\circ \) означает, что центральный угол, опирающийся на дугу \( AB \), равен \( 90^\circ \).
— Равенство \( KC = LD \) гарантирует симметрию конструкции, что важно для корректного вычисления площади.
— Перпендикулярность \( EF \) и \( AB \) обеспечивает правильную геометрическую интерпретацию задачи.

Все шаги доказательства строго следуют из данных условий и свойств геометрических фигур.