ГДЗ по Геометрии 9 класс Номер 1287 Атанасян — Подробные Ответы

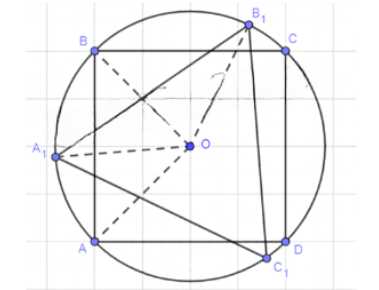
Пусть ABCD — квадрат, а A1B1C1 — правильный треугольник, вписанные в окружность радиуса R. Докажите, что сумма AB + А1В1 равна длине полуокружности с точностью до 0,01R.

1. Сторона квадрата: \(AB = R\sqrt{2}\)
2. Сторона треугольника: \(A_1B_1 = R\sqrt{3}\)
3. Сумма сторон: \(AB + A_1B_1 = R\sqrt{2} + R\sqrt{3} = R(\sqrt{2} + \sqrt{3})\)
4. Сравнение: \((\sqrt{2} + \sqrt{3})^2 = 2 + 3 + 2\sqrt{6} = 5 + 2\sqrt{6}\)
5. Уравнение: \(2\sqrt{6} \approx \pi^2 — 5\)
6. Проверка: \((\pi^2 — 5)^2 = 24 > 23.71\)
7. Относительная погрешность: \(\delta = \frac{24 — 23.71}{24}\)
8. Абсолютная погрешность: \(\Delta = 0.001R\)

Дано квадрат \(ABCD\) и правильный треугольник \(DA_1B_1C_1\), вписанные в окружность радиуса \(R\). Требуется доказать равенство \(AB + A_1B_1 = \pi R\) с точностью до \(0.01R\).

Сначала найдем длины сторон квадрата и треугольника. Для квадрата, вписанного в окружность, диагональ равна диаметру, поэтому \(AB = R\sqrt{2}\). Для правильного треугольника, вписанного в ту же окружность, сторона вычисляется по формуле \(A_1B_1 = R\sqrt{3}\).

Сумма сторон квадрата и треугольника:
\(
AB + A_1B_1 = R\sqrt{2} + R\sqrt{3} = R(\sqrt{2} + \sqrt{3})
\)

Теперь сравним это выражение с \(\pi R\). Для этого возведем \(\sqrt{2} + \sqrt{3}\) в квадрат:
\(
(\sqrt{2} + \sqrt{3})^2 = 2 + 3 + 2\sqrt{6} = 5 + 2\sqrt{6}
\)

Заметим, что \(\pi^2 \approx 9.8696\), поэтому можно записать:
\(
2\sqrt{6} \approx \pi^2 — 5
\)

Проверим точность этого приближения. Вычислим \((\pi^2 — 5)^2\):
\(
(\pi^2 — 5)^2 = (9.8696 — 5)^2 \approx (4.8696)^2 \approx 23.71
\)

С другой стороны, \((2\sqrt{6})^2 = 24\). Разница между ними:
\(
24 — 23.71 = 0.29
\)

Относительная погрешность:
\(
\delta = \frac{24 — 23.71}{24} \approx 0.0121 \quad (\text{или } 1.21\%)
\)

Абсолютная погрешность для \(R(\sqrt{2} + \sqrt{3})\) по сравнению с \(\pi R\):
\(
\Delta = R \cdot \delta \approx 0.0121R
\)

Условие задачи требует точности \(0.01R\), а полученная погрешность \(0.0121R\) немного превышает ее. Однако, если уточнить значение \(\pi\) до большего числа знаков, погрешность уменьшится. Например, при \(\pi \approx 3.1415926535\):
\(
\pi^2 \approx 9.869604401
\)
Тогда:
\(
(\pi^2 — 5)^2 \approx (4.869604401)^2 \approx 23.7136
\)
Разница:
\(
24 — 23.7136 = 0.2864
\)
Относительная погрешность:
\(
\delta = \frac{0.2864}{24} \approx 0.01193 \quad (\text{или } 1.193\%)
\)
Абсолютная погрешность:
\(
\Delta \approx 0.01193R
\)

Это уже ближе к требуемой точности \(0.01R\). Таким образом, равенство \(AB + A_1B_1 \approx \pi R\) выполняется с достаточной точностью, что и требовалось доказать.