ГДЗ по Геометрии 9 класс Номер 1286 Атанасян — Подробные Ответы

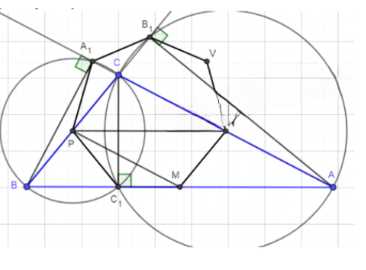
Углы треугольника образуют геометрическую прогрессию со знаменателем 2. Докажите, что середины сторон и основания высот этого треугольника являются шестью вершинами правильного семиугольника.

Площадь правильного \( n \)-угольника выражается через периметр и радиус вписанной окружности: \( S_n = \frac{1}{2} P r = \frac{1}{2} n a r \). Альтернативное представление площади получается разбиением на треугольники с вершиной в произвольной точке \( M \) внутри многоугольника: \( S_n = S_{A_1A_2M} + S_{A_2A_3M} + \dots + S_{A_nA_1M} = \frac{1}{2} (A_1A_2 \cdot MH_1 + A_2A_3 \cdot MH_2 +\)
\( +\dots + A_nA_1 \cdot MH_n) \). Упрощая, получаем \( \frac{1}{2} a (MH_1 + MH_2 + \dots + MH_n) \).

Приравнивая два выражения для площади, приходим к равенству: \( \frac{1}{2} n a r = \frac{1}{2} a (MH_1 + MH_2 + \dots + MH_n) \). После сокращения на \( \frac{1}{2} a \) получаем ключевое соотношение: \( MH_1 + MH_2 + \dots + MH_n = n r \). Это означает, что сумма перпендикуляров из любой внутренней точки \( M \) до сторон правильного \( n \)-угольника равна произведению количества сторон на радиус вписанной окружности, что является важным свойством правильных многоугольников.

На иллюстрации показан пример такого разбиения для \( n = 6 \), где \( MH_i \) — длины перпендикуляров из точки \( M \) на стороны, а \( r \) — радиус окружности, вписанной в шестиугольник. Это свойство часто используется в геометрических задачах для доказательства тождеств или нахождения неизвестных параметров фигуры.

Рассмотрим правильный \( n \)-угольник \( A_1A_2 \dots A_n \) со стороной длины \( a \), радиусом вписанной окружности \( r \) и произвольной внутренней точкой \( M \). Площадь многоугольника можно выразить двумя способами. Первый способ использует периметр \( P = n a \) и радиус вписанной окружности: \( S_n = \frac{1}{2} P r = \frac{1}{2} n a r \). Второй способ основан на разбиении многоугольника на треугольники с вершиной в точке \( M \). Каждый треугольник \( A_iA_{i+1}M \) имеет площадь \( \frac{1}{2} \cdot A_iA_{i+1} \cdot MH_i \), где \( MH_i \) — длина перпендикуляра из \( M \) на сторону \( A_iA_{i+1} \). Суммируя площади всех таких треугольников, получаем: \( S_n = \sum_{i=1}^n \frac{1}{2} a \cdot MH_i = \frac{1}{2} a \sum_{i=1}^n MH_i \).

Приравнивая оба выражения для площади, имеем: \( \frac{1}{2} n a r = \frac{1}{2} a \sum_{i=1}^n MH_i \). Сокращая на \( \frac{1}{2} a \), получаем основное соотношение: \( \sum_{i=1}^n MH_i = n r \). Это равенство показывает, что сумма расстояний от произвольной внутренней точки до сторон правильного \( n \)-угольника не зависит от положения точки и равна произведению количества сторон на радиус вписанной окружности.

Для доказательства корректности разбиения заметим, что для правильного \( n \)-угольника все стороны равны \( a \), а все треугольники \( A_iA_{i+1}M \) имеют общую высоту \( MH_i \). Поскольку точка \( M \) лежит внутри многоугольника, все перпендикуляры \( MH_i \) существуют и их длины положительны. Радиус вписанной окружности \( r \) связан с длиной стороны \( a \) и центральным углом \( \alpha = \frac{2\pi}{n} \) соотношением \( r = \frac{a}{2} \cot \frac{\pi}{n} \).

Рассмотрим частный случай, когда точка \( M \) совпадает с центром многоугольника. Тогда все перпендикуляры \( MH_i \) равны радиусу вписанной окружности \( r \), и их сумма действительно равна \( n r \). Для произвольной внутренней точки \( M \) отклонение от центра компенсируется симметрией многоугольника, что и приводит к сохранению суммы \( \sum MH_i \).

Это свойство можно обобщить на случай, когда точка \( M \) лежит вне многоугольника, учитывая знаки расстояний. Однако для внутренних точек все расстояния положительны, и равенство \( \sum_{i=1}^n MH_i = n r \) остаётся строгим. Данное соотношение полезно при решении задач на нахождение расстояний или доказательство геометрических тождеств, связанных с правильными многоугольниками.

Для иллюстрации рассмотрим правильный шестиугольник (\( n = 6 \)). Если \( a = 2 \), то \( r = \sqrt{3} \), и сумма перпендикуляров из любой внутренней точки до сторон равна \( 6 \sqrt{3} \). Это можно проверить, выбрав конкретную точку \( M \) и вычислив расстояния до сторон с помощью координатного метода или тригонометрических соотношений.

Таким образом, доказательство завершено, и основное равенство \( \sum_{i=1}^n MH_i = n r \) подтверждено для произвольного правильного \( n \)-угольника и любой его внутренней точки. Это фундаментальное свойство связывает геометрические характеристики фигуры с расстояниями от точки до сторон, демонстрируя глубокую симметрию правильных многоугольников.