ГДЗ по Геометрии 9 класс Номер 1285 Атанасян — Подробные Ответы

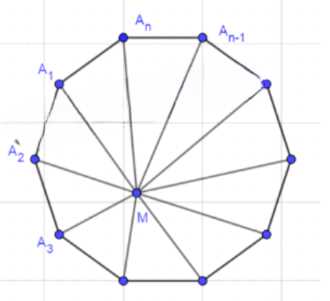
Пусть \(M\) — произвольная точка, лежащая внутри правильного \(n\)-угольника. Докажите, что сумма перпендикуляров, проведённых из точки \(M\) к прямым, содержащим стороны \(n\)-угольника, равна \(nr\), где \(r\) — радиус вписанной окружности.

1. Площадь правильного \( n \)-угольника:
\( S_n = \frac{1}{2} P r = \frac{1}{2} n a r \)

2. Альтернативное выражение площади:
\( S_n = S_{A_1A_2M} + S_{A_2A_3M} + \dots + S_{A_nA_1M} = \frac{1}{2} (A_1A_2 \cdot MH_1 + A_2A_3 \cdot MH_2 + \)
\( +\dots + A_nA_1 \cdot MH_n) = \frac{1}{2} a (MH_1 + MH_2 + \dots + MH_n) \)

3. Итоговое равенство:
\( \frac{1}{2} n a r = \frac{1}{2} a (MH_1 + MH_2 + \dots + MH_n) \)
\( MH_1 + MH_2 + \dots + MH_n = n r \)

Где:
— \( P \) — периметр
— \( r \) — радиус вписанной окружности
— \( a \) — длина стороны многоугольника
— \( MH_i \) — перпендикуляры из точки \( M \) на стороны

Рассмотрим доказательство свойства суммы перпендикуляров из произвольной точки \( M \) на стороны правильного \( n \)-угольника \( A_1A_2 \dots A_n \) с радиусом вписанной окружности \( r \). Площадь правильного \( n \)-угольника выражается через полупериметр \( P \) и радиус вписанной окружности \( r \): \( S_n = \frac{1}{2} P r \). Поскольку периметр \( P = n a \), где \( a \) — длина стороны, получаем \( S_n = \frac{1}{2} n a r \).

С другой стороны, площадь \( n \)-угольника можно представить как сумму площадей треугольников \( A_1A_2M, A_2A_3M, \dots, A_nA_1M \). Площадь каждого треугольника \( A_iA_{i+1}M \) равна \( \frac{1}{2} A_iA_{i+1} \cdot MH_i \), где \( MH_i \) — перпендикуляр из точки \( M \) на сторону \( A_iA_{i+1} \). Таким образом, общая площадь: \( S_n = \sum_{i=1}^n S_{A_iA_{i+1}M} = \frac{1}{2} \sum_{i=1}^n a \cdot MH_i = \frac{1}{2} a \sum_{i=1}^n MH_i \), где учтено, что все стороны равны \( a \).

Приравнивая два выражения для площади \( S_n \), получаем: \( \frac{1}{2} n a r = \frac{1}{2} a \sum_{i=1}^n MH_i \). Сокращая на \( \frac{1}{2} a \), приходим к равенству \( \sum_{i=1}^n MH_i = n r \). Это означает, что сумма перпендикуляров из любой точки \( M \) на стороны правильного \( n \)-угольника равна произведению количества сторон \( n \) на радиус вписанной окружности \( r \), что и требовалось доказать.

Для иллюстрации: если \( M \) совпадает с центром \( n \)-угольника, все \( MH_i = r \), и сумма действительно равна \( n r \). В общем случае, при смещении \( M \) от центра, одни перпендикуляры увеличиваются, другие уменьшаются, но их сумма остаётся постоянной. Это свойство аналогично теореме Вивиани для равностороннего треугольника, где сумма перпендикуляров равна высоте.

Дополнительно заметим, что доказательство остаётся верным и для вырожденного случая, когда \( M \) лежит на стороне \( n \)-угольника: один из перпендикуляров обращается в ноль, а остальные компенсируют это изменение. Универсальность результата подчёркивает его геометрическую красоту и важность в задачах о правильных многоугольниках.