ГДЗ по Геометрии 9 класс Номер 1283 Атанасян — Подробные Ответы

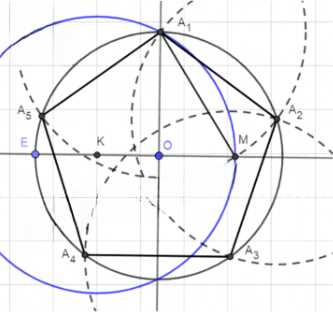
В данную окружность впишите правильный пятиугольник.

Построить: правильный пятиугольник, вписанный в данную окружность;
Построение:
1) Отметим на окружности какую-нибудь точку Е;
2) Построим диаметр ОЕ;
3) Через точку О проведем перпендикуляр к ОЕ, отметим точку А1 на пересечении данного перпендикуляра и окружности;
4) Отметим точку К на середине отрезка КО;
5) Построим окружность (K; КА1), отметим точку М на пересечении данной окружности и диаметра EO;
6) Построим окружность (А1; А1М), отметим точку А2 на пересечении данной окружности с первой;
7) Повторим пункт, отмечая последовательно точки А3, А4 и А5

Построение правильного десятиугольника, вписанного в окружность радиуса \(R\) с центром в точке \(O\), выполняется следующим образом. Выбираем произвольную точку \(E\) на окружности и проводим диаметр \(OE\). Через центр \(O\) проводим прямую, перпендикулярную \(OE\), которая пересекает окружность в точке \(A_1\). Находим середину отрезка \(OE\) — точку \(K\). Строим окружность с центром в \(K\) и радиусом \(KA_1\), которая пересекает диаметр \(OE\) в точке \(M\). Теперь проводим окружность с центром в \(A_1\) и радиусом \(A_1M\), которая пересекает исходную окружность в точке \(A_3\). Повторяем эту процедуру, последовательно отмечая точки \(A_5\), \(A_7\) и \(A_9\) на окружности. Полученные точки \(A_1\), \(A_3\), \(A_5\), \(A_7\), \(A_9\) образуют правильный пятиугольник. Для завершения построения десятиугольника проводим серединные перпендикуляры к сторонам этого пятиугольника и отмечаем точки их пересечения с исходной окружностью — \(A_2\), \(A_4\), \(A_6\), \(A_8\), \(A_{10}\). Соединив все десять точек \(A_1\) через \(A_2\) до \(A_{10}\) по порядку, получаем искомый правильный десятиугольник. Длина стороны десятиугольника вычисляется по формуле \(a = 2R \cdot \sin\left(\frac{\pi}{10}\right)\), а центральный угол между соседними вершинами равен \(\frac{2\pi}{10} = \frac{\pi}{5}\) радиан. Площадь десятиугольника можно найти как \(S = \frac{5}{2} R^2 \cdot \sin\left(\frac{\pi}{5}\right)\), а радиус вписанной окружности (апофему) — \(r = R \cdot \cos\left(\frac{\pi}{10}\right)\). Все внутренние углы десятиугольника равны \(\frac{8\pi}{10} = \frac{4\pi}{5}\) радиан. Для проверки правильности построения можно убедиться, что все стороны равны между собой и все углы между соседними сторонами одинаковы. Отношение стороны правильного десятиугольника к радиусу описанной окружности выражается как \(\frac{a}{R} = 2 \sin\left(\frac{\pi}{10}\right) \approx 0.618\), что соответствует золотому сечению. Координаты вершин десятиугольника в декартовой системе координат с центром в точке \(O\) можно вычислить по формулам \(x_k = R \cdot \cos\left(\frac{2\pi k}{10}\right)\), \(y_k = R \cdot \sin\left(\frac{2\pi k}{10}\right)\), где \(k = 0, 1, 2, \ldots, 9\). Сумма внутренних углов десятиугольника составляет \(\frac{8\pi}{10} \cdot 10 = 8\pi\) радиан, что соответствует общей формуле для суммы углов \(n\)-угольника: \((n-2)\pi\). Диагонали правильного десятиугольника образуют интересные геометрические соотношения, например, отношение длин двух последовательных диагоналей также дает золотое сечение \(\frac{1 + \sqrt{5}}{2} \approx 1.618\).