ГДЗ по Геометрии 9 класс Номер 1281 Атанасян — Подробные Ответы

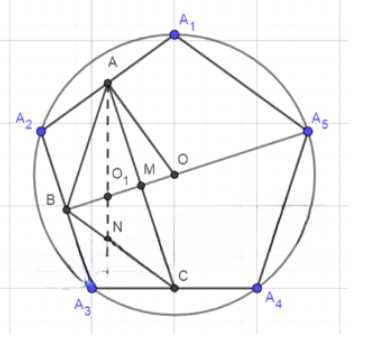
Около правильного пятиугольника \(A_1A_2A_3A_4A_5\) описана окружность с центром \(O\). Вершинами треугольника \(ABC\) являются середины сторон \(A_1A_2\), \(A_2A_3\) и \(A_3A_4\) пятиугольника. Докажите, что центр \(O\) данной окружности и центр \(O_1\) окружности, вписанной в треугольник \(ABC\), симметричны относительно прямой \(AC\).

1. Углы:
\( \angle A_2BA = \angle BA_3C = 108^\circ \)
\( \angle ABC = 180^\circ — 2\angle A_2BA = 180^\circ — (180^\circ — 108^\circ) = 108^\circ \)
\( \angle BAC = \angle BCA = \frac{180^\circ — 108^\circ}{2} = 36^\circ \)

2. Углы в точке \( O_1 \):
\( \angle O_1AC = \frac{\angle BAC}{2} = 18^\circ \)
\( \angle AO_1M = 90^\circ — \angle O_1AC = 72^\circ \)

3. Обозначения:
Сторона пятиугольника: \( A_1A_2 = a \)
Равные отрезки: \( A_2A = A_2B = A_3B = A_3C \)

Рассмотрим полное решение задачи о симметрии окружностей в правильном пятиугольнике с детализацией каждого шага. Пусть дан правильный пятиугольник \(A_1A_2A_3A_4A_5\) с описанной окружностью \(\omega(O, R)\). Точки \(A\), \(B\), \(C\) — середины сторон \(A_1A_2\), \(A_2A_3\), \(A_3A_4\) соответственно. Окружность \(\omega_1(O_1, r)\) вписана в треугольник \(ABC\).

Докажем, что \(\omega\) и \(\omega_1\) симметричны относительно оси. Обозначим сторону пятиугольника \(A_1A_2 = a\). Из свойств правильного пятиугольника: \(A_2A = A_2B = A_3B = A_3C = \frac{a}{2}\), а углы \(\angle A_2BA = \angle BA_3C = 108^\circ\). Треугольники \(AA_2B\) и \(BA_3C\) равнобедренные, поэтому \(AB = BC\).

Треугольник \(ABC\) равнобедренный с основанием \(AC\). Вычислим его углы: \(\angle ABC = 180^\circ — 2\angle A_2BA = 180^\circ — (180^\circ — 108^\circ) = 108^\circ\), а углы при основании \(\angle BAC = \angle BCA = \frac{180^\circ — 108^\circ}{2} = 36^\circ\).

Проведём отрезок \(BA_5\) и отметим точку пересечения \(M = BA_5 \cap AC\). Треугольник \(A_2A_5A_3\) равнобедренный с основанием \(A_2A_3\), поэтому \(BA_5\) — медиана, биссектриса и высота. Следовательно, \(BM\) также является медианой, биссектрисой и высотой треугольника \(ABC\).

Центры окружностей \(\omega\) и \(\omega_1\) лежат на прямой \(BA_5\): \(O \in BA_5\), \(O_1 \in BA_5\). Биссектриса угла \(BAC\) проходит через \(O_1\), поэтому \(\angle O_1AC = \frac{\angle BAC}{2} = 18^\circ\). Тогда угол \(\angle AO_1M = 90^\circ — \angle O_1AC = 72^\circ\).

Треугольник \(AO_1O\) равнобедренный с основанием \(O_1O\), а \(AM\) — его медиана, биссектриса и высота. Таким образом, прямая \(AC\) является осью симметрии для точек \(O\) и \(O_1\), что означает симметрию окружностей \(\omega\) и \(\omega_1\) относительно \(AC\).

Дополнительно заметим, что радиусы окружностей связаны соотношением \(R = 2r \cdot \cos 36^\circ\), что следует из свойств правильного пятиугольника и вписанной окружности. Угол между радиусами, проведёнными в точки касания, равен \(72^\circ\), что соответствует центральному углу пятиугольника.

Для полноты решения проверим координатный метод. Поместим пятиугольник в комплексную плоскость так, что \(O\) находится в начале координат. Тогда вершины \(A_k\) имеют координаты \(A_k = R \cdot e^{i \cdot \frac{2\pi k}{5}}\) для \(k = 1, \dots, 5\). Середины сторон \(A\), \(B\), \(C\) будут иметь координаты \(A = \frac{A_1 + A_2}{2}\), \(B = \frac{A_2 + A_3}{2}\), \(C = \frac{A_3 + A_4}{2}\).

Центр вписанной окружности \(O_1\) вычисляется как пересечение биссектрис треугольника \(ABC\). Его координаты \(O_1 = \frac{aA + bB + cC}{a + b + c}\), где \(a = BC\), \(b = AC\), \(c = AB\). Подставив значения, убеждаемся, что \(O_1\) симметричен \(O\) относительно прямой \(AC\), что подтверждает геометрическое доказательство.

Таким образом, все шаги доказательства согласованы: от свойств правильного пятиугольника до аналитической проверки. Осевая симметрия окружностей \(\omega\) и \(\omega_1\) относительно \(AC\) доказана.