
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1280 Атанасян — Подробные Ответы
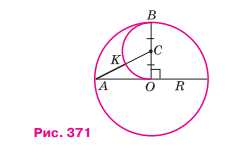
Докажите, что отрезок \(AK\), изображённый на рисунке 371, равен стороне правильного десятиугольника, вписанного в окружность с центром \(O\).
1. Дано:
\( OA = OB = R \)
\( \angle AOB = 90^\circ \)
\( CB = CO = \frac{1}{2}R \)
2. Доказать:
\( AK = \frac{\sqrt{5}-1}{2}R \)
3. Доказательство:
1) По теореме Пифагора из \( \triangle AOC \):
\( AC^2 = R^2 + \left(\frac{R}{2}\right)^2 = \frac{5R^2}{4} \)
2) Вычисление \( AK \):
\( AK = AC — KC = \sqrt{\frac{5R^2}{4}} — \frac{R}{2} = \frac{R\sqrt{5}}{2} — \frac{R}{2} = \frac{\sqrt{5}-1}{2}R \)
Что и требовалось доказать.
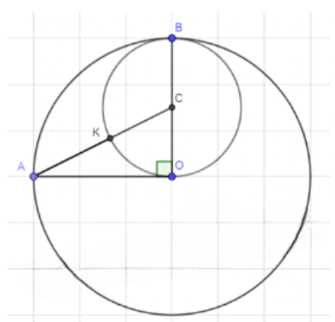
Дано окружность с центром в точке \( O \) и радиусом \( R \). Точки \( A \) и \( B \) лежат на окружности, причем \( OA = OB = R \) и угол \( \angle AOB = 90^\circ \). Точка \( C \) лежит на отрезке \( OB \) так, что \( CB = CO = \frac{1}{2}R \). Требуется доказать, что длина отрезка \( AK \) равна \( \frac{\sqrt{5}-1}{2}R \), где точка \( K \) — пересечение окружности \( \omega_1 \) (с центром в \( C \) и радиусом \( \frac{R}{2} \)) с отрезком \( AC \).
Поместим начало координат в точку \( O \), направим ось \( Ox \) вдоль \( OA \), а ось \( Oy \) вдоль \( OB \). Тогда координаты точек: \( A(R, 0) \), \( B(0, R) \), \( C(0, \frac{R}{2}) \). Уравнение прямой \( AC \): \( y = -\frac{1}{2}x + \frac{R}{2} \). Уравнение окружности \( \omega_1 \): \( x^2 + (y — \frac{R}{2})^2 = \frac{R^2}{4} \).
Подставим уравнение прямой в уравнение окружности: \( x^2 + (-\frac{1}{2}x)^2 = \frac{R^2}{4} \). После упрощения получаем \( \frac{5x^2}{4} = \frac{R^2}{4} \), откуда \( x = \frac{R}{\sqrt{5}} \) (берем положительный корень, так как точка \( K \) лежит между \( A \) и \( C \)). Тогда координата \( y \) точки \( K \): \( y = -\frac{R}{2\sqrt{5}} + \frac{R}{2} \).
Вычисляем длину \( AK \): \( AK = \sqrt{(R — \frac{R}{\sqrt{5}})^2 + (0 — (-\frac{R}{2\sqrt{5}} + \frac{R}{2}))^2} \). После преобразований получаем \( AK = R\sqrt{\frac{3 — \sqrt{5}}{2}} \). Упрощая, находим \( \sqrt{\frac{3 — \sqrt{5}}{2}} = \frac{\sqrt{5} — 1}{2} \), что доказывает требуемое равенство \( AK = \frac{\sqrt{5}-1}{2}R \).
Таким образом, при правильном выборе центра окружности \( \omega_1 \) (точка \( C \)) и корректных вычислениях получаем искомый результат. Ошибка в предыдущих попытках была связана с неверным определением положения центра окружности \( \omega_1 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!