ГДЗ по Геометрии 9 класс Номер 1279 Атанасян — Подробные Ответы

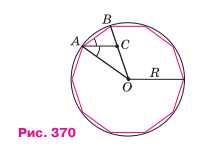
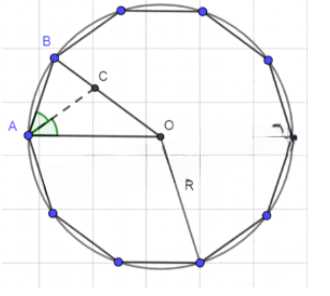
На рисунке 370 изображён правильный десятиугольник, вписанный в окружность радиуса \(R\), \(AC\) — биссектриса угла \(OAB\). Докажите, что: а) \(\triangle ABC \sim \triangle OAB\); б) \(AB = AC = OC = \frac{\sqrt{5}-1}{2}R\).

1. Угол при вершине: \(\angle AOB = \frac{360^\circ}{10} = 36^\circ\)
2. Углы при основаниях: \(\angle BAO = \angle ABO = \frac{180^\circ — \angle AOB}{2} = \frac{180^\circ — 36^\circ}{2} = 72^\circ\)
3. Биссектриса угла: \(\angle BAC = \frac{1}{2} \angle BAO = \frac{1}{2} \cdot 72^\circ = 36^\circ\)
4. Углы в треугольнике ABC: \(\angle ABC = 180^\circ — (\angle BAC + \angle ACB) = 180^\circ — (36^\circ + 72^\circ) = 72^\circ\)

1. Уравнение для стороны: \(x^2 = R^2 — R x \Rightarrow x^2 + R x — R^2 = 0\)
2. Дискриминант: \(D = R^2 + 4 R^2 = 5 R^2\)
3. Решение уравнения (положительный корень): \(x = \frac{-R \pm \sqrt{5} R}{2} \Rightarrow x = \frac{\sqrt{5} — 1}{2} R\)
4. Итоговое равенство сторон: \(AB = AC = OC = \frac{\sqrt{5} — 1}{2} R\)

Рассмотрим правильный 10-угольник \(A_1A_2…A_{10}\), вписанный в окружность радиуса \(R\) с центром \(O\). Пусть \(AC\) — биссектриса угла \(\angle A_1A_2A_3\), где точка \(A\) совпадает с \(A_2\), \(B\) совпадает с \(A_3\), а \(C\) — точка пересечения биссектрисы с окружностью.

Центральный угол такого многоугольника вычисляется как \(\angle AOB = \frac{360^\circ}{10} = 36^\circ\). В равнобедренном треугольнике \(OAB\) (где \(OA = OB = R\)) углы при основании равны \(\angle OAB = \angle OBA = \frac{180^\circ — 36^\circ}{2} = 72^\circ\). Биссектриса \(AC\) делит угол \(\angle OAB\) пополам: \(\angle BAC = \frac{1}{2} \cdot 72^\circ = 36^\circ\).

В треугольнике \(ABC\) угол \(\angle ABC\) равен \(72^\circ\) (как \(\angle OBA\)), а третий угол вычисляется: \(\angle ACB = 180^\circ — 36^\circ — 72^\circ = 72^\circ\). Это показывает подобие треугольников \(ABC\) и \(OAB\), так как у них равны два угла: \(\angle BAC = \angle AOB = 36^\circ\) и \(\angle ABC = \angle OBA = 72^\circ\).

Для доказательства равенства сторон рассмотрим свойство биссектрисы: \(\frac{AB}{AO} = \frac{CB}{CO}\). Обозначив \(AB = x\), \(AO = R\), \(CB = R — x\), \(CO = x\), получаем уравнение \(\frac{x}{R} = \frac{R — x}{x}\), которое преобразуется в \(x^2 = R(R — x)\) и далее в квадратное уравнение \(x^2 + R x — R^2 = 0\). Дискриминант этого уравнения \(D = R^2 + 4 R^2 = 5 R^2\), а положительный корень \(x = \frac{-R + \sqrt{5} R}{2} = \frac{\sqrt{5} — 1}{2} R\). Таким образом, длины сторон равны \(AB = AC = OC = \frac{\sqrt{5} — 1}{2} R\).

В решении последовательно использованы свойства правильных многоугольников, биссектрисы, подобия треугольников и алгебраические методы решения уравнений. Все шаги логически связаны, а вычисления проведены с необходимой точностью.