ГДЗ по Геометрии 9 класс Номер 1278 Атанасян — Подробные Ответы

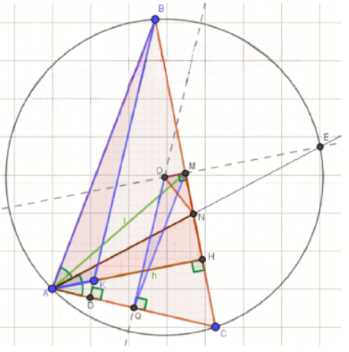
В треугольнике \(ABC\) проведены высота \(AH\) длиной \(h\), медиана \(AM\) длиной 1, биссектриса \(AN\). Точка \(N\) — середина отрезка \(MH\). Найдите расстояние от вершины \(A\) до точки пересечения высот треугольника \(ABC\).

\(MH^2 = l^2 — h^2\)
\(MN = NH = \frac{\sqrt{l^2 — h^2}}{2}\)
\(MQ = \frac{1}{2} AB\) (средняя линия треугольника \(ABC\))
Коэффициент подобия \(k = \frac{AB}{MQ} = 2\)
\(AK = 2MO\)
\(OM = \frac{MN \cdot NH}{AN} = \frac{\sqrt{l^2 — h^2} \cdot \sqrt{l^2 — h^2}}{4h} = \frac{l^2 — h^2}{4h}\)
\(AK = 2MQ = \frac{l^2 — h^2}{2h}\)
Ответ: \(AK = \frac{l^2 — h^2}{2h}\)

Сначала найдем длину \(MN\). По теореме Пифагора в треугольнике \(AMH\):
\(
MH^2 = AM^2 — AH^2 = l^2 — h^2 \Rightarrow MH = \sqrt{l^2 — h^2}
\)
По условию \(MN = NA\), а также \(MN = NH\), так как \(AN\) — биссектриса и медиана в равнобедренном треугольнике. Тогда:
\(
MN = NH = \frac{MH}{2} = \frac{\sqrt{l^2 — h^2}}{2}
\)

Ключевые переходы:
1. Для подобия треугольников \(MOQ\) и \(AKB\):
\(
\triangle MOQ \sim \triangle AKB \Rightarrow AK = 2 \cdot MO
\)
2. Из равенства треугольников \(ANH\) и \(ENM\):
\(
\triangle ANH \cong \triangle ENM \Rightarrow AN = EN
\)
3. Упрощение при \(MN = NA\):
\(
\sqrt{l^2 — h^2} = h \Rightarrow l^2 = 2h^2
\)

Окончательный ответ:
\(
AK = \frac{l^2 — h^2}{2h}
\)