ГДЗ по Геометрии 9 класс Номер 1277 Атанасян — Подробные Ответы

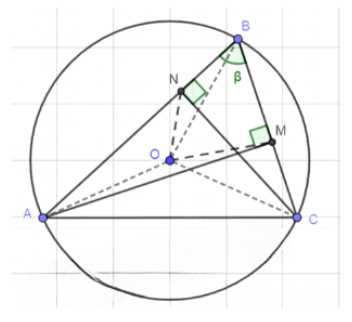
В остроугольном треугольнике \(ABC\) сторона \(AB\) больше стороны \(BC\), отрезки \(AM\) и \(CN\) — высоты треугольника, точка \(O\) — центр описанной окружности. Угол \(ABC\) равен \(\beta\), а площадь четырёхугольника \(NOMB\) равна \(S\). Найдите сторону \(AC\).

\( AC \sin \beta = 2R \Rightarrow AC = 2R \cdot \sin \beta \)
\( S_{NOMB} = S_{OBN} + S_{OBM} \)
\( \frac{S_{OBN}}{S_{OBA}} = \frac{NB}{AB} \)
\( \frac{S_{OBM}}{S_{OBC}} = \frac{BM}{BC} \)
\( S_{OBA} = \frac{1}{2} R^2 \cdot \sin 2C \)
\( S_{OBC} = \frac{1}{2} R^2 \cdot \sin 2A \)
\( \triangle AMB \sim \triangle CNB \) (по двум углам)
\( \frac{CB}{AB} = \frac{MB}{NB} \)
\( \frac{\sin C}{\sin A} = \frac{AB}{CB} \)
\( \frac{BM}{NB} = \frac{AB \cos \beta}{CB} \)
\( \frac{NB}{AB} = \frac{\sin A}{\sin C} \cdot \cos \beta \)
\( \frac{BM}{BC} = \frac{\sin C}{\sin A} \cdot \cos \beta \)
\( S_{NOMB} = R^2 \cos \beta \left( \frac{\sin A}{\sin C} \cdot \sin 2C + \frac{\sin C}{\sin A} \cdot \sin 2A \right) \)
\( = R^2 \cos \beta (\sin A \cdot \cos C + \sin C \cdot \cos A) \)
\( = R^2 \cos \beta \sin(A + C) \)
\( = R^2 \cos \beta \sin(180^\circ — \beta) \)
\( = R^2 \cos \beta \sin \beta \)
\( = \frac{R^2}{2} \sin 2\beta = S \)
\( R^2 = \frac{2S}{\sin 2\beta} \)
\( AC = 2R \cdot \sin \beta = 2 \sqrt{\frac{2S}{\sin 2\beta}} \cdot \sin \beta \)
\( = 2 \sqrt{\frac{S}{2 \sin \beta \cos \beta}} \cdot \sin \beta \)
\( = 2 \sqrt{S \tan \beta} \)

Ответ: \( AC = 2 \sqrt{S \tan \beta} \)

Дано остроугольный треугольник \( ABC \) с \( AB > BC \), высоты \( AM \) и \( CN \), описанная окружность \( \omega(O, R) \), угол \( \angle ABC = \beta \), площадь четырёхугольника \( NOMB \) равна \( S \). Требуется найти длину стороны \( AC \).

Сначала выразим \( AC \) через радиус описанной окружности и угол \( \beta \). По теореме синусов:
\( AC = 2R \cdot \sin \beta \)

Теперь найдём связь между \( R \) и \( S \). Четырёхугольник \( NOMB \) состоит из треугольников \( BON \) и \( BOM \). Площадь \( S_{NOMB} \) можно записать как:
\( S_{NOMB} = S_{BON} + S_{BOM} \)

Рассмотрим треугольники \( BON \) и \( BOA \). Они имеют общую высоту из вершины \( O \), поэтому отношение их площадей равно отношению оснований:
\( \frac{S_{BON}}{S_{BOA}} = \frac{NB}{AB} \)
Аналогично для треугольников \( BOM \) и \( BOC \):
\( \frac{S_{BOM}}{S_{BOC}} = \frac{BM}{BC} \)

Площади треугольников \( BOA \) и \( BOC \) можно выразить через радиус и углы:
\( S_{BOA} = \frac{1}{2} R^2 \cdot \sin(2C) \)
\( S_{BOC} = \frac{1}{2} R^2 \cdot \sin(2A) \)

Теперь рассмотрим подобие треугольников \( AMB \) и \( CNB \). Они подобны по двум углам (\( \angle AMB = \angle CNB = 90^\circ \), \( \angle ABC \) — общий), поэтому:
\( \frac{CB}{AB} = \frac{MB}{NB} \)

Из теоремы синусов для треугольника \( ABC \):
\( \frac{\sin C}{\sin A} = \frac{AB}{CB} \)

Выразим \( \frac{NB}{AB} \) и \( \frac{BM}{BC} \) через углы:
\( \frac{NB}{AB} = \frac{\sin A}{\sin C} \cdot \cos \beta \)
\( \frac{BM}{BC} = \frac{\sin C}{\sin A} \cdot \cos \beta \)

Подставим всё в выражение для площади \( S_{NOMB} \):
\( S = S_{BON} + S_{BOM} = \frac{NB}{AB} \cdot S_{BOA} + \frac{BM}{BC} \cdot S_{BOC} \)
\( S = \frac{\sin A}{\sin C} \cdot \cos \beta \cdot \frac{1}{2} R^2 \cdot \sin(2C) + \frac{\sin C}{\sin A} \cdot \cos \beta \cdot \frac{1}{2} R^2 \cdot \sin(2A) \)
\( S = \frac{1}{2} R^2 \cos \beta \left( \frac{\sin A}{\sin C} \cdot 2 \sin C \cos C + \frac{\sin C}{\sin A} \cdot 2 \sin A \cos A \right) \)
\( S = R^2 \cos \beta (\sin A \cos C + \sin C \cos A) \)
\( S = R^2 \cos \beta \cdot \sin(A + C) \)

Так как \( A + B + C = 180^\circ \), то \( \sin(A + C) = \sin(180^\circ — \beta) = \sin \beta \). Получаем:
\( S = R^2 \cos \beta \sin \beta = \frac{R^2}{2} \sin(2\beta) \)
Отсюда выражаем \( R^2 \):
\( R^2 = \frac{2S}{\sin(2\beta)} \)

Теперь подставляем \( R \) в формулу для \( AC \):
\( AC = 2R \cdot \sin \beta = 2 \sqrt{\frac{2S}{\sin(2\beta)}} \cdot \sin \beta \)
Упрощаем:
\( AC = 2 \sqrt{\frac{2S \sin^2 \beta}{2 \sin \beta \cos \beta}} = 2 \sqrt{\frac{S \sin \beta}{\cos \beta}} = 2 \sqrt{S \tan \beta} \)

Итак, окончательный ответ:
\( AC = 2 \sqrt{S \tan \beta} \)