ГДЗ по Геометрии 9 класс Номер 1275 Атанасян — Подробные Ответы

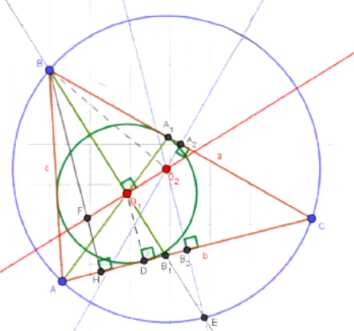
Докажите, что стороны треугольника образуют арифметическую прогрессию тогда и только тогда, когда прямая, проходящая через центры вписанной и описанной окружностей, перпендикулярна к одной из биссектрис треугольника.

1. Условие вписанности:

Четырёхугольник \(ABCD\) вписан в окружность \(\Rightarrow \angle A + \angle C = 180^\circ\) и \(\angle B + \angle D = 180^\circ\).

2. Формула Брахмагупты:
Площадь вычисляется через полупериметр \(p = \frac{a + b + c + d}{2}\):
\(
S = \sqrt{(p — a)(p — b)(p — c)(p — d)}.
\)

3. Ключевые шаги вывода:
— Применяем теорему косинусов к треугольникам \(ABD\) и \(CBD\) для диагонали \(BD\):
\(
BD^2 = a^2 + d^2 — 2ad \cos A = b^2 + c^2 + 2bc \cos A \quad (\text{так как } \cos C = -\cos A).
\)
— Находим \(\cos A\):
\(
\cos A = \frac{a^2 + d^2 — b^2 — c^2}{2(ad + bc)}.
\)
— Выражаем \(\sin A\) через тождество \(\sin^2 A = 1 — \cos^2 A\) и раскладываем числитель:
\(
\sin A = \frac{2\sqrt{(p — a)(p — b)(p — c)(p — d)}}{ad + bc}.
\)
— Площадь как сумма площадей треугольников \(ABD\) и \(CBD\):
\(
S = \frac{1}{2}(ad + bc)\sin A = \sqrt{(p — a)(p — b)(p — c)(p — d)}.
\)

Итог: Формула Брахмагупты доказана через тригонометрические преобразования и свойства вписанных четырёхугольников.

Рассмотрим полное решение задачи о площади вписанного четырёхугольника с детализацией каждого шага. Пусть дан четырёхугольник \(ABCD\) со сторонами \(a, b, c, d\), вписанный в окружность. По условию вписанного четырёхугольника сумма противоположных углов равна \(180^\circ\): \(\angle A + \angle C = 180^\circ\) и \(\angle B + \angle D = 180^\circ\). Для вычисления площади воспользуемся формулой Брахмагупты: \(S = \sqrt{(p — a)(p — b)(p — c)(p — d)}\), где \(p = \frac{a + b + c + d}{2}\) — полупериметр.

Начнём с применения теоремы косинусов к треугольникам \(ABD\) и \(CBD\) для нахождения диагонали \(BD\). В треугольнике \(ABD\): \(BD^2 = a^2 + d^2 — 2ad \cos A\). В треугольнике \(CBD\): \(BD^2 = b^2 + c^2 — 2bc \cos C\). Учитывая, что \(\angle C = 180^\circ — \angle A\), подставим \(\cos C = -\cos A\) во второе уравнение: \(BD^2 = b^2 + c^2 + 2bc \cos A\). Приравниваем выражения для \(BD^2\): \(a^2 + d^2 — 2ad \cos A = b^2 + c^2 + 2bc \cos A\). Переносим все члены в одну сторону: \(a^2 + d^2 — b^2 — c^2 = 2(ad + bc) \cos A\). Отсюда выражаем \(\cos A\): \(\cos A = \frac{a^2 + d^2 — b^2 — c^2}{2(ad + bc)}\).

Теперь найдём \(\sin A\) через основное тригонометрическое тождество: \(\sin^2 A = 1 — \cos^2 A = 1 — \left( \frac{a^2 + d^2 — b^2 — c^2}{2(ad + bc)} \right)^2\). Приводим к общему знаменателю: \(\sin^2 A = \frac{4(ad + bc)^2 — (a^2 + d^2 — b^2 — c^2)^2}{4(ad + bc)^2}\). Числитель раскладываем как разность квадратов: \(4(ad + bc)^2 — (a^2 + d^2 — b^2 — c^2)^2 = (2ad + 2bc — a^2 — d^2 + b^2 + c^2)\)
\((2ad + 2bc + a^2 + d^2 — b^2 — c^2)\).
Группируем слагаемые: первый множитель \((b^2 + c^2 + 2bc) — (a^2 + d^2 — 2ad) = (b + c)^2 — (a — d)^2\), второй множитель \((a^2 + d^2 + 2ad) — (b^2 + c^2 — 2bc) = (a + d)^2 — (b — c)^2\).
Таким образом, \(\sin^2 A = \frac{(b + c)^2 — (a — d)^2)((a + d)^2 — (b — c)^2)}{4(ad + bc)^2}\).

Раскрываем скобки в числителе, используя разность квадратов: \((b + c)^2 — (a — d)^2 = (b + c — a + d)(b + c + a — d)\), \((a + d)^2 — (b — c)^2 = (a + d — b + c)(a + d + b — c)\).
Обозначим периметр \(P = a + b + c + d\), тогда выражения можно переписать как: \((P — 2a)(P — 2d)\) и \((P — 2b)(P — 2c)\). Подставляем полупериметр \(p = \frac{P}{2}\): \(\sin^2 A = \frac{(2p — 2a)(2p — 2b)(2p — 2c)(2p — 2d)}{4(ad + bc)^2} = \frac{16(p — a)(p — b)(p — c)(p — d)}{4(ad + bc)^2} = \)
\(\frac{4(p — a)(p — b)(p — c)(p — d)}{(ad + bc)^2}\).
Извлекаем квадратный корень: \(\sin A = \frac{2\sqrt{(p — a)(p — b)(p — c)(p — d)}}{ad + bc}\).

Площадь четырёхугольника \(ABCD\) равна сумме площадей треугольников \(ABD\) и \(CBD\): \(S = S_{ABD} + S_{CBD} = \frac{1}{2} ad \sin A + \frac{1}{2} bc \sin C\). Учитывая, что \(\angle C = 180^\circ — \angle A\), получаем \(\sin C = \sin A\), поэтому \(S = \frac{1}{2} (ad + bc) \sin A\).
Подставляем выражение для \(\sin A\): \(S = \frac{1}{2} (ad + bc) \cdot \frac{2\sqrt{(p — a)(p — b)(p — c)(p — d)}}{ad + bc} = \sqrt{(p — a)(p — b)(p — c)(p — d)}\). Таким образом, мы получили формулу Брахмагупты для площади вписанного четырёхугольника.