ГДЗ по Геометрии 9 класс Номер 1273 Атанасян — Подробные Ответы

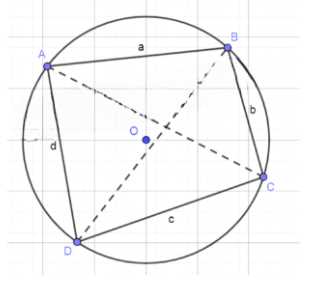
Выразите диагонали вписанного в окружность четырёхугольника через его стороны.

1. Свойство вписанного четырёхугольника:
\( \angle A + \angle C = 180^\circ \)
\( \angle B + \angle D = 180^\circ \)

2. Теорема косинусов:
\( AC^2 = a^2 + b^2 — 2ab \cos B \)
\( AC^2 = c^2 + d^2 — 2cd \cos D = c^2 + d^2 + 2cd \cos B \)
\( a^2 + b^2 — 2ab \cos B = c^2 + d^2 + 2cd \cos B \)
\( 2(ab + cd) \cos B = a^2 + b^2 — c^2 — d^2 \)
\( \cos B = \frac{a^2 + b^2 — c^2 — d^2}{2(ab + cd)} \)
\( AC^2 = a^2 + b^2 — 2ab \cdot \frac{a^2 + b^2 — c^2 — d^2}{2(ab + cd)} \)
\( AC = \sqrt{\frac{cd(a^2 + b^2) + ab(c^2 + d^2)}{ab + cd}} \)

3. Для второй диагонали:
\( BD^2 = a^2 + d^2 — 2ad \cos A \)
\( BD^2 = b^2 + c^2 — 2bc \cos A = b^2 + c^2 + 2bc \cos A \)
\( a^2 + d^2 — 2ad \cos A = b^2 + c^2 + 2bc \cos A \)
\( 2(ad + bc) \cos A = a^2 + d^2 — b^2 — c^2 \)
\( \cos A = \frac{a^2 + d^2 — b^2 — c^2}{2(ad + bc)} \)
\( BD^2 = a^2 + d^2 — 2ad \cdot \frac{a^2 + d^2 — b^2 — c^2}{2(ad + bc)} \)
\( BD = \sqrt{\frac{bc(a^2 + d^2) + ad(b^2 + c^2)}{ad + bc}} \)

Ответ:
\( AC = \sqrt{\frac{cd(a^2 + b^2) + ab(c^2 + d^2)}{ab + cd}} \)
\( BD = \sqrt{\frac{bc(a^2 + d^2) + ad(b^2 + c^2)}{ad + bc}} \)

Рассмотрим вписанный четырёхугольник \(ABCD\) в окружности радиуса \(R\) с заданными сторонами: \(AB = a\), \(BC = b\), \(CD = c\), \(AD = d\). Для нахождения длин диагоналей \(AC\) и \(BD\) воспользуемся свойствами вписанного четырёхугольника и теоремой косинусов.

Сумма противоположных углов вписанного четырёхугольника равна \(180^\circ\):
\(
\angle A + \angle C = 180^\circ, \quad \angle B + \angle D = 180^\circ.
\)
Это позволяет выразить косинусы одних углов через другие, так как \(\cos(180^\circ — x) = -\cos x\).

Применим теорему косинусов для треугольника \(ABC\):
\(
AC^2 = a^2 + b^2 — 2ab \cos B.
\)
Аналогично для треугольника \(ADC\):
\(
AC^2 = c^2 + d^2 — 2cd \cos D = c^2 + d^2 + 2cd \cos B,
\)
поскольку \(\cos D = \cos(180^\circ — B) = -\cos B\).

Приравниваем выражения для \(AC^2\):
\(
a^2 + b^2 — 2ab \cos B = c^2 + d^2 + 2cd \cos B.
\)
Переносим все слагаемые в одну сторону:
\(
a^2 + b^2 — c^2 — d^2 = 2(ab + cd) \cos B.
\)
Отсюда находим \(\cos B\):
\(
\cos B = \frac{a^2 + b^2 — c^2 — d^2}{2(ab + cd)}.
\)

Подставляем \(\cos B\) обратно в выражение для \(AC^2\):
\(
AC^2 = a^2 + b^2 — 2ab \cdot \frac{a^2 + b^2 — c^2 — d^2}{2(ab + cd)}.
\)
Упрощаем:
\(
AC^2 = \frac{(a^2 + b^2)(ab + cd) — ab(a^2 + b^2 — c^2 — d^2)}{ab + cd}.
\)
Раскрываем скобки и группируем слагаемые:
\(
AC^2 = \frac{cd(a^2 + b^2) + ab(c^2 + d^2)}{ab + cd}.
\)
Окончательно получаем длину диагонали \(AC\):
\(
AC = \sqrt{\frac{cd(a^2 + b^2) + ab(c^2 + d^2)}{ab + cd}}.
\)

Аналогично находим диагональ \(BD\). Рассмотрим треугольники \(ABD\) и \(CBD\):
\(
BD^2 = a^2 + d^2 — 2ad \cos A,
\)
\(
BD^2 = b^2 + c^2 — 2bc \cos C = b^2 + c^2 + 2bc \cos A,
\)
поскольку \(\cos C = \cos(180^\circ — A) = -\cos A\).

Приравниваем выражения для \(BD^2\):
\(
a^2 + d^2 — 2ad \cos A = b^2 + c^2 + 2bc \cos A.
\)
Переносим слагаемые:
\(
a^2 + d^2 — b^2 — c^2 = 2(ad + bc) \cos A.
\)
Находим \(\cos A\):
\(
\cos A = \frac{a^2 + d^2 — b^2 — c^2}{2(ad + bc)}.
\)

Подставляем \(\cos A\) в выражение для \(BD^2\):
\(
BD^2 = a^2 + d^2 — 2ad \cdot \frac{a^2 + d^2 — b^2 — c^2}{2(ad + bc)}.
\)
Упрощаем:
\(
BD^2 = \frac{(a^2 + d^2)(ad + bc) — ad(a^2 + d^2 — b^2 — c^2)}{ad + bc}.
\)
Раскрываем скобки и группируем:
\(
BD^2 = \frac{bc(a^2 + d^2) + ad(b^2 + c^2)}{ad + bc}.
\)
Окончательно получаем длину диагонали \(BD\):
\(
BD = \sqrt{\frac{bc(a^2 + d^2) + ad(b^2 + c^2)}{ad + bc}}.
\)

Таким образом, искомые диагонали выражаются через стороны четырёхугольника следующим образом:
\(
AC = \sqrt{\frac{cd(a^2 + b^2) + ab(c^2 + d^2)}{ab + cd}}, \quad BD = \sqrt{\frac{bc(a^2 + d^2) + ad(b^2 + c^2)}{ad + bc}}.
\)