ГДЗ по Геометрии 9 класс Номер 1272 Атанасян — Подробные Ответы

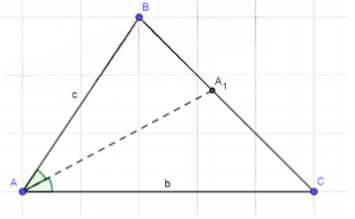
Докажите, что в треугольнике ABC биссектриса \(AA_1\) вычисляется по формуле \(AA_1 = \frac{2bc \cos \frac{A}{2}}{b+c}\), где \(b = AC\), \(c = AB\).

1) Площадь треугольника:
\(S_{\triangle ABC} = S_{\triangle ABA_1} + S_{\triangle AA_1C}\)

2) Формула площади через синус угла:
\(\frac{1}{2} bc \cdot \sin A = \frac{1}{2} (b + c) \cdot AA_1 \cdot \sin \frac{A}{2}\)

3) Выражение для \(AA_1\):
\(AA_1 = \frac{2bc \cdot \sin \frac{A}{2} \cdot \cos \frac{A}{2}}{(b + c) \cdot \sin \frac{A}{2}} = \frac{2bc \cdot \cos \frac{A}{2}}{b + c}\)

4) Итоговая формула:
\(AA_1 = \frac{2b \cdot \cos \frac{A}{2}}{b + c}\)

Дано треугольник \(ABC\) с биссектрисой \(AA_1\), где \(AC = b\), \(AB = c\). Требуется доказать, что длина биссектрисы \(AA_1\) выражается формулой:
\(AA_1 = \frac{2bc \cdot \cos \frac{A}{2}}{b + c}\)

Начнем с выражения площадей треугольников через стороны и углы. Площадь треугольника \(ABC\) можно записать как сумму площадей треугольников \(ABA_1\) и \(AA_1C\):
\(S_{ABC} = S_{ABA_1} + S_{AA_1C}\)
Используем формулу площади через две стороны и синус угла между ними:
\(\frac{1}{2} \cdot AB \cdot AC \cdot \sin A = \frac{1}{2} \cdot AB \cdot AA_1 \cdot \sin \frac{A}{2} + \frac{1}{2} \cdot AC \cdot AA_1 \cdot \sin \frac{A}{2}\)
Подставляем известные значения \(AB = c\) и \(AC = b\):
\(\frac{1}{2} \cdot b \cdot c \cdot \sin A = \frac{1}{2} \cdot c \cdot AA_1 \cdot \sin \frac{A}{2} + \frac{1}{2} \cdot b \cdot AA_1 \cdot \sin \frac{A}{2}\)
Упрощаем уравнение, сокращая \(\frac{1}{2}\) и вынося \(AA_1 \cdot \sin \frac{A}{2}\) за скобки:
\(b \cdot c \cdot \sin A = AA_1 \cdot \sin \frac{A}{2} \cdot (b + c)\)

Теперь выразим \(\sin A\) через \(\sin \frac{A}{2}\) и \(\cos \frac{A}{2}\), используя формулу двойного угла:
\(\sin A = 2 \cdot \sin \frac{A}{2} \cdot \cos \frac{A}{2}\)
Подставляем это в предыдущее уравнение:
\(b \cdot c \cdot 2 \cdot \sin \frac{A}{2} \cdot \cos \frac{A}{2} = AA_1 \cdot \sin \frac{A}{2} \cdot (b + c)\)
Сокращаем \(\sin \frac{A}{2}\) с обеих сторон (поскольку \(\sin \frac{A}{2} \neq 0\)):
\(2 \cdot b \cdot c \cdot \cos \frac{A}{2} = AA_1 \cdot (b + c)\)

Осталось выразить \(AA_1\):
\(AA_1 = \frac{2 \cdot b \cdot c \cdot \cos \frac{A}{2}}{b + c}\)

Таким образом, мы получили искомую формулу для длины биссектрисы \(AA_1\) в треугольнике \(ABC\). Формула доказана.

Дополнительно можно заметить, что данное выражение симметрично относительно сторон \(b\) и \(c\), что соответствует геометрическому смыслу биссектрисы как линии, делящей угол на две равные части и пропорционально делящей противоположную сторону. Также стоит отметить, что если \(b = c\) (треугольник равнобедренный), то формула упрощается до \(AA_1 = b \cdot \cos \frac{A}{2}\), что согласуется с ожидаемым результатом для равнобедренного треугольника.