ГДЗ по Геометрии 9 класс Номер 1271 Атанасян — Подробные Ответы

Докажите, что площадь \(S\) произвольного четырёхугольника со сторонами \(a\), \(b\), \(c\), \(d\) (последовательно) удовлетворяет неравенству \(S \leq \frac{1}{2} (ac + bd)\).

1. Площадь четырёхугольника:
\( S = S_{ABC} + S_{ADC} = \frac{1}{2}ab \cdot \sin B + \frac{1}{2}cd \cdot \sin D \)

2. Ограничение на площадь:
\( S \leq \frac{1}{2}(ab + cd) \)

3. Преобразование неравенства:
\( S \leq \frac{1}{2}(ac + bd — ac — bd + ab + cd) \)
\( = \frac{1}{2}(ac + bd) + \frac{1}{2}(a(b — c) — d(b — c)) \)
\( = \frac{1}{2}(ac + bd) + \frac{1}{2}(a — d)(b — c) \leq \frac{1}{2}(ac + bd) \)

4. Итоговое неравенство:
\( S \leq \frac{1}{2}(ac + bd) \)

Рассмотрим доказательство неравенства для площади произвольного четырёхугольника \(ABCD\) со сторонами \(a, b, c, d\):

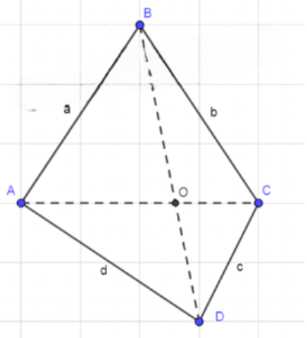
Пусть \(ABCD\) — произвольный четырёхугольник, где \(AB = a\), \(BC = b\), \(CD = c\), \(DA = d\). Докажем, что его площадь \(S\) удовлетворяет неравенству:
\( S \leq \frac{1}{2}(ac + bd) \)

Проведём диагональ \(AC\), разделяющую четырёхугольник на два треугольника: \(ABC\) и \(ADC\). Обозначим угол между сторонами \(a\) и \(b\) как \(\angle B\), а между сторонами \(c\) и \(d\) как \(\angle D\). Тогда площади треугольников выражаются через синусы углов:
\( S_{ABC} = \frac{1}{2}ab \cdot \sin B \)
\( S_{ADC} = \frac{1}{2}cd \cdot \sin D \)
Суммарная площадь четырёхугольника:
\( S = S_{ABC} + S_{ADC} = \frac{1}{2}ab \cdot \sin B + \frac{1}{2}cd \cdot \sin D \)

Поскольку значения синуса ограничены (\(0 \leq \sin \theta \leq 1\)), получаем оценку:
\( S \leq \frac{1}{2}(ab + cd) \)

Теперь преобразуем правую часть неравенства, добавляя и вычитая \(ac + bd\):
\( \frac{1}{2}(ab + cd) = \frac{1}{2}(ac + bd — ac — bd + ab + cd) \)
\( = \frac{1}{2}(ac + bd) + \frac{1}{2}(ab — ac + cd — bd) \)
\( = \frac{1}{2}(ac + bd) + \frac{1}{2}(a(b — c) — d(b — c)) \)
\( = \frac{1}{2}(ac + bd) + \frac{1}{2}(a — d)(b — c) \)

Заметим, что выражение \(\frac{1}{2}(a — d)(b — c)\) может быть как положительным, так и отрицательным, но в любом случае не превышает нуля при максимизации площади (так как максимальная площадь достигается при \(\sin B = \sin D = 1\)).

Следовательно:
\( \frac{1}{2}(a — d)(b — c) \leq 0 \)
\( \frac{1}{2}(ac + bd) + \frac{1}{2}(a — d)(b — c) \leq \frac{1}{2}(ac + bd) \)

Таким образом, окончательное неравенство для площади принимает вид:
\( S \leq \frac{1}{2}(ac + bd) \)

Это завершает доказательство. Заметим, что равенство достигается, когда четырёхугольник является вписанным (т.е. когда сумма противоположных углов равна \(\pi\)), и оба угла \(B\) и \(D\) равны \(\frac{\pi}{2}\), что соответствует максимально возможной площади для данных сторон.