ГДЗ по Геометрии 9 класс Номер 1270 Атанасян — Подробные Ответы

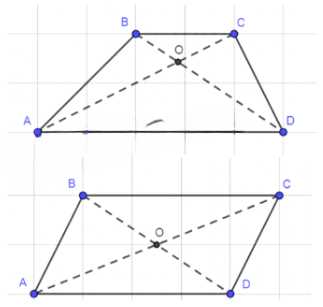
Диагонали AC и BD четырёхугольника ABCD пересекаются в точке O. Площадь треугольника ODC есть среднее пропорциональное между площадями треугольников OBC и OAD. Докажите, что ABCD — трапеция с основаниями AD и BC или параллелограмм.

1. Площадь треугольника \(S_{ODC} = \frac{1}{2} \cdot OC \cdot OD \cdot \sin \alpha\)
2. Площадь треугольника \(S_{OBC} = \frac{1}{2} \cdot OB \cdot OC \cdot \sin (180^\circ — \alpha)\)
3. Уравнение площадей \(\sqrt{S_{OBC} \cdot S_{OAD}} = S_{ODC}\)
4. Преобразованное уравнение \(\left(\frac{1}{2} cd \sin \alpha\right)^2 = \left(\frac{1}{2} bc \sin \alpha\right) \cdot \left(\frac{1}{2} ad \sin \alpha\right)\)
5. Упрощение \(c^2d^2 = bc \cdot ad\)
6. Коэффициент подобия \(k = \frac{c}{b} = \frac{a}{d}\)
7. Отношения сторон \(\frac{OC}{OA} = k\) и \(\frac{OB}{OD} = k\)

Также в тексте присутствуют геометрические обозначения:
— Точки пересечения диагоналей \(AC \cap BD = O\)
— Обозначения векторов \(OA = a\), \(OB = b\), \(OC = c\), \(OD = d\)
— Угол \(\angle COD = \alpha\)

Дано: четырёхугольник \(ABCD\), диагонали \(AC\) и \(BD\) пересекаются в точке \(O\), причём выполняется условие \(S_{ODC} = \sqrt{S_{OBC} \cdot S_{OAD}}\). Требуется доказать, что \(ABCD\) — трапеция или параллелограмм.

Введём обозначения: \(OA = a\), \(OB = b\), \(OC = c\), \(OD = d\), \(\angle COD = \alpha\). Рассмотрим площади треугольников, образованных диагоналями. Площадь треугольника \(ODC\) выражается как \(S_{ODC} = \frac{1}{2} \cdot OC \cdot OD \cdot \sin \alpha = \frac{1}{2} cd \sin \alpha\). Площадь треугольника \(OBC\) равна \(S_{OBC} = \frac{1}{2} \cdot OB \cdot OC \cdot \sin (180^\circ — \alpha) = \frac{1}{2} bc \sin \alpha\), так как \(\sin (180^\circ — \alpha) = \sin \alpha\). Аналогично, площадь треугольника \(OAD\) будет \(S_{OAD} = \frac{1}{2} \cdot OA \cdot OD \cdot \sin \alpha = \frac{1}{2} ad \sin \alpha\).

По условию задачи \(S_{ODC} = \sqrt{S_{OBC} \cdot S_{OAD}}\). Подставим выражения для площадей: \(\frac{1}{2} cd \sin \alpha = \sqrt{\frac{1}{2} bc \sin \alpha \cdot \frac{1}{2} ad \sin \alpha}\). Упростим правую часть: \(\sqrt{\frac{1}{4} abcd \sin^2 \alpha} = \frac{1}{2} \sqrt{abcd} \sin \alpha\). Таким образом, получаем уравнение \(\frac{1}{2} cd \sin \alpha = \frac{1}{2} \sqrt{abcd} \sin \alpha\), которое после сокращения на \(\frac{1}{2} \sin \alpha\) даёт \(cd = \sqrt{abcd}\). Возведём обе части в квадрат: \(c^2 d^2 = abcd\). Разделим обе части на \(cd\) (при условии \(cd \neq 0\)): \(cd = ab\).

Теперь выразим отношения сторон: \(\frac{c}{b} = \frac{a}{d} = k\), где \(k\) — некоторый коэффициент подобия. Заметим, что \(\angle BOC = \angle DOA\) как вертикальные углы. Таким образом, треугольники \(BOC\) и \(DOA\) подобны по второму признаку подобия (пропорциональность двух сторон и равенство углов между ними). Из подобия следует, что \(\angle CBO = \angle ADO\), а значит, прямые \(AD\) и \(BC\) параллельны, так как эти углы являются накрест лежащими при секущей \(BD\).

Рассмотрим возможные значения коэффициента \(k\). Если \(k < 1\), то треугольник \(BOC\) меньше треугольника \(DOA\), и сторона \(BC\) меньше стороны \(AD\), что соответствует трапеции \(ABCD\) с основаниями \(BC\) и \(AD\). Если \(k = 1\), то треугольники \(BOC\) и \(DOA\) равны, откуда следует равенство сторон \(BC = AD\) и \(AB = CD\), то есть \(ABCD\) — параллелограмм. Если \(k > 1\), то треугольник \(BOC\) больше треугольника \(DOA\), и сторона \(BC\) больше стороны \(AD\), что также соответствует трапеции \(ABCD\), но с основаниями \(AD\) и \(BC\).

Таким образом, четырёхугольник \(ABCD\) является либо трапецией (если \(k \neq 1\)), либо параллелограммом (если \(k = 1\)), что и требовалось доказать.