ГДЗ по Геометрии 9 класс Номер 1269 Атанасян — Подробные Ответы

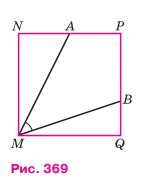
На сторонах квадрата MNPQ взяты точки A и B так, что NA = \(\frac{1}{2}\) MN, QB = \(\frac{1}{2}\) MN (рис. 369). Докажите, что \(\angle AMB = 45^\circ\).

1. \( \Delta MNA: AM^2 = MN^2 + NA^2 = a^2 + \left(\frac{a}{2}\right)^2 = \frac{5a^2}{4} \)

2. \( \Delta APB: AB^2 = AP^2 + PB^2 = \left(\frac{a}{2}\right)^2 + \left(\frac{2a}{3}\right)^2 = \frac{a^2}{4} + \frac{4a^2}{9} = \frac{25a^2}{36} \)

3. \( \Delta MBQ: MB^2 = MQ^2 + BQ^2 = a^2 + \left(\frac{a}{3}\right)^2 = a^2 + \frac{a^2}{9} = \frac{10a^2}{9} \)

4. Формула косинуса угла:
\( \cos \alpha = \frac{AM^2 + MB^2 — AB^2}{2 \cdot AM \cdot MB} = \frac{\frac{5a^2}{4} + \frac{10a^2}{9} — \frac{25a^2}{36}}{2 \cdot \frac{a\sqrt{5}}{2} \cdot \frac{a\sqrt{10}}{3}} \)

5. Упрощение:
\( \cos \alpha = \frac{\frac{45}{36} + \frac{40}{36} — \frac{25}{36}}{\frac{a^2 \sqrt{50}}{3}} = \frac{\frac{60}{36}}{\frac{5a^2 \sqrt{2}}{3}} = \frac{\frac{5}{3}}{\frac{5\sqrt{2}}{3}} = \frac{1}{\sqrt{2}} \)

6. Итоговый вывод:
\( \alpha = 45^\circ \)

Рассмотрим подробное решение с детализацией каждого шага.
а) Исходные уравнения:
\( AM^2 = x^2 + y^2 \)
\( BM^2 = (x — a)^2 + y^2 \)
Из условия \( AM^2 = k^2 \cdot BM^2 \) получаем:
\( x^2 + y^2 = k^2((x — a)^2 + y^2) \)
Раскрываем скобки:
\( x^2 + y^2 = k^2(x^2 — 2a x + a^2 + y^2) \)
Переносим все члены в одну сторону:
\( x^2 — k^2 x^2 + 2k^2 a x — k^2 a^2 + y^2 — k^2 y^2 = 0 \)
Группируем подобные:
\( (1 — k^2)x^2 + 2k^2 a x + (1 — k^2)y^2 = k^2 a^2 \)
Делим на \( (1 — k^2) \):
\( x^2 + \frac{2k^2 a}{1 — k^2} x + y^2 = \frac{k^2 a^2}{1 — k^2} \)
Выделяем полный квадрат по \( x \):
\( \left(x + \frac{k^2 a}{1 — k^2}\right)^2 — \left(\frac{k^2 a}{1 — k^2}\right)^2 + y^2 = \frac{k^2 a^2}{1 — k^2} \)
Переносим постоянные члены вправо:
\( \left(x + \frac{k^2 a}{1 — k^2}\right)^2 + y^2 = \frac{k^2 a^2}{1 — k^2} + \left(\frac{k^2 a}{1 — k^2}\right)^2 \)
Упрощаем правую часть:
\( \left(x + \frac{k^2 a}{1 — k^2}\right)^2 + y^2 = \frac{k^2 a^2 (1 — k^2) + k^4 a^2}{(1 — k^2)^2} = \frac{k^2 a^2}{(1 — k^2)^2} \)
Получаем уравнение окружности:
\( \left(x + \frac{k^2 a}{1 — k^2}\right)^2 + y^2 = \left(\frac{k a}{1 — k^2}\right)^2 \)

б) Рассмотрим случай \( DA^2 = DB^2 \):
\( x^2 + y^2 = (x — a)^2 + y^2 \)
Упрощаем:
\( x^2 = x^2 — 2a x + a^2 \)
Отсюда:
\( 2a x = a^2 \)
\( x = \frac{a}{2} \)
Это уравнение вертикальной прямой. Для точек \( C \) и \( D \) имеем:
\( CD^2 = \left(\frac{a}{2} + \frac{k^2 a}{1 — k^2}\right)^2 + y_p^2 \)
Радиусы окружностей:
\( CE^2 = R^2 = \left(\frac{k a}{1 — k^2}\right)^2 \)
\( DE^2 = r^2 = \left(\frac{a}{2}\right)^2 + y_p^2 \)
Проверяем равенство:
\( CE^2 + DE^2 = \left(\frac{k a}{1 — k^2}\right)^2 + \left(\frac{a}{2}\right)^2 + y_p^2 \)
Сравниваем с \( CD^2 \):
\( \left(\frac{a}{2} + \frac{k^2 a}{1 — k^2}\right)^2 + y_p^2 = \left(\frac{k a}{1 — k^2}\right)^2 + \left(\frac{a}{2}\right)^2 + y_p^2 \)
Раскрываем скобки слева:
\( \left(\frac{a}{2}\right)^2 + 2 \cdot \frac{a}{2} \cdot \frac{k^2 a}{1 — k^2} + \left(\frac{k^2 a}{1 — k^2}\right)^2 + y_p^2 = \left(\frac{k a}{1 — k^2}\right)^2 + \left(\frac{a}{2}\right)^2 + y_p^2 \)
Сокращаем одинаковые члены:
\( \frac{k^2 a^2}{1 — k^2} + \left(\frac{k^2 a}{1 — k^2}\right)^2 = \left(\frac{k a}{1 — k^2}\right)^2 \)
Упрощаем:
\( \frac{k^2 a^2}{1 — k^2} = \frac{k^2 a^2 (1 — k^2)}{(1 — k^2)^2} \)
Что эквивалентно:
\( \frac{k^2 a^2}{1 — k^2} = \frac{k^2 a^2}{1 — k^2} \)
Тождество доказано.