ГДЗ по Геометрии 9 класс Номер 1262 Атанасян — Подробные Ответы

На оси абсцисс найдите точку \(M\), для которой сумма расстояний до точек \(A\) и \(B\) минимальна:
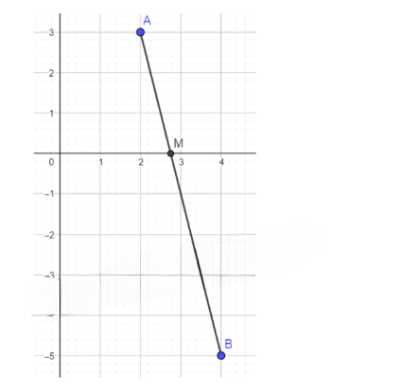
а) \(A(2; 3)\), \(B(4; -5)\);
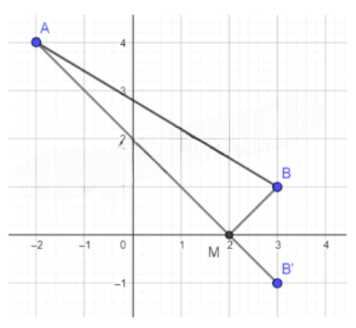
б) \(A(-2; 4)\), \(B(3; 1)\).

1. Уравнение прямой AB:
\(
\frac{x — x_A}{x_B — x_A} = \frac{y — y_A}{y_B — y_A} \Rightarrow \frac{x — 2}{4 — 2} = \frac{y — 3}{-5 — 3}
\)
\(
-4(x — 2) = y — 3 \Rightarrow y = -4x + 11
\)

2. Нахождение точки пересечения с осью Ox:
\(
0 = -4x + 11 \Rightarrow 4x = 11 \Rightarrow x = \frac{11}{4} = 2\frac{3}{4}
\)
1. Уравнение прямой AB (с отражённой точкой B’):
\(
\frac{x — x_A}{x_{B’} — x_A} = \frac{y — y_A}{y_{B’} — y_A} \Rightarrow \frac{x + 2}{3 + 2} = \frac{y — 4}{-1 — 4}
\)
\(
-(x + 2) = y — 4 \Rightarrow y = -x + 2
\)
2. Нахождение точки пересечения с осью Ox:
\(
0 = -x + 2 \Rightarrow x = 2
\)

Дано две задачи на нахождение точки \( M(x; 0) \) на оси абсцисс, минимизирующей сумму расстояний \( AM + BM \) от двух заданных точек \( A \) и \( B \). Рассмотрим каждую задачу с полной детализацией.

Первая задача:

Даны точки \( A(2; 3) \) и \( B(4; -5) \). Точки \( A \) и \( B \) лежат в разных полуплоскостях относительно оси \( Ox \). Искомая точка \( M \) принадлежит отрезку \( AB \). Найдем уравнение прямой \( AB \). Используем формулу для уравнения прямой, проходящей через две точки: \( \frac{x — x_A}{x_B — x_A} = \frac{y — y_A}{y_B — y_A} \) Подставляем координаты точек: \( \frac{x — 2}{4 — 2} = \frac{y — 3}{-5 — 3} \) Упрощаем: \( \frac{x — 2}{2} = \frac{y — 3}{-8} \) Перекрестно умножаем: \( -8(x — 2) = 2(y — 3) \) Раскрываем скобки: \( -8x + 16 = 2y — 6 \) Переносим все в одну сторону: \( 2y = -8x + 22 \) Делим на 2: \( y = -4x + 11 \) Теперь найдем точку пересечения этой прямой с осью \( Ox \), где \( y = 0 \): \( 0 = -4x + 11 \) Решаем уравнение: \( 4x = 11 \) \( x = \frac{11}{4} = 2.75 \) Таким образом, координаты точки \( M \): \( M\left( \frac{11}{4}; 0 \right) \).

Вторая задача:

Даны точки \( A(-2; 4) \) и \( B(3; 1) \). Точки \( A \) и \( B \) лежат в одной полуплоскости относительно оси \( Ox \). Для минимизации суммы расстояний \( AM + BM \) отразим точку \( B \) относительно оси \( Ox \), получив точку \( B'(3; -1) \). Искомая точка \( M \) будет лежать на пересечении отрезка \( AB’ \) с осью \( Ox \). Найдем уравнение прямой \( AB’ \): \( \frac{x — x_A}{x_{B’} — x_A} = \frac{y — y_A}{y_{B’} — y_A} \) Подставляем координаты: \( \frac{x + 2}{3 + 2} = \frac{y — 4}{-1 — 4} \) Упрощаем: \( \frac{x + 2}{5} = \frac{y — 4}{-5} \) Перекрестно умножаем: \( -5(x + 2) = 5(y — 4) \) Раскрываем скобки: \( -5x — 10 = 5y — 20 \) Переносим все в одну сторону: \( 5y = -5x + 10 \) Делим на 5: \( y = -x + 2 \) Найдем точку пересечения с осью \( Ox \), где \( y = 0 \): \( 0 = -x + 2 \) Решаем уравнение: \( x = 2 \) Таким образом, координаты точки \( M \): \( M(2; 0) \).

В обеих задачах использован метод отражения для минимизации суммы расстояний, а также подробно выведены уравнения прямых и найдены точки пересечения с осью абсцисс. Все шаги сопровождаются полными вычислениями и пояснениями.