
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1260 Атанасян — Подробные Ответы
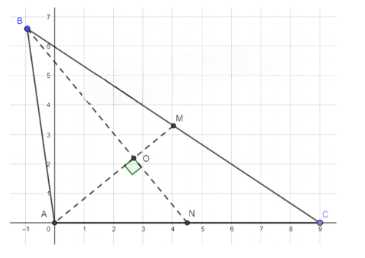
В треугольнике \(ABC\) стороны \(AC = 9\) см, \(BC = 12\) см. Медианы \(AM\) и \(BN\) взаимно перпендикулярны. Найдите длину стороны \(AB\).
Дано треугольник \(ABC\) с \(AC = 9\) см, \(BC = 12\) см. Медианы \(AM\) и \(BN\) перпендикулярны (\(AM \perp BN\)). Координаты точек: \(A(0; 0)\), \(C(9; 0)\), \(B(x; y)\) (\(y > 0\)). Координаты точки \(N\): \(\left(\frac{x + 9}{2}; \frac{y}{2}\right)\). Условие перпендикулярности векторов: \(\overrightarrow{AM} \cdot \overrightarrow{BN} = 0\), что приводит к уравнению \((x + 9)(x — 2) + y^2 = 0\) или \(x^2 + 5x — 2 + y^2 = 0\).
Точка \(B\) также лежит на окружности с центром \(C(9; 0)\) и радиусом \(12\): \((x — 9)^2 + y^2 = 144\). Решая систему уравнений \((x — 9)^2 + y^2 = 144\) и \(\left(x + \frac{9}{2}\right)^2 + y^2 = \frac{729}{16}\), находим \(x = -1\). Подставляя \(x\) во второе уравнение, получаем \(y = 2\sqrt{11}\).
Искомое расстояние \(AB\) вычисляется как \(\sqrt{(-1)^2 + (2\sqrt{11})^2} = \sqrt{45} = 3\sqrt{5}\) см. Ответ: \(AB = 3\sqrt{5}\) см.
Рассмотрим задачу о треугольнике \(ABC\) с данными \(AC = 9\) см и \(BC = 12\) см, где медианы \(AM\) и \(BN\) перпендикулярны. Для решения используем координатный метод, поместив точку \(A\) в начало координат \((0; 0)\), а точку \(C\) на оси абсцисс \((9; 0)\). Координаты точки \(B\) обозначим как \((x; y)\), причем \(y > 0\).
Медиана \(AM\) проходит из вершины \(A\) в середину стороны \(BC\). Координаты точки \(M\) вычисляются как среднее арифметическое координат точек \(B\) и \(C\):
\(M\left(\frac{x + 9}{2}; \frac{y}{2}\right)\).
Медиана \(BN\) проводится из вершины \(B\) в середину стороны \(AC\). Координаты точки \(N\):
\(N\left(\frac{9}{2}; 0\right)\).
Условие перпендикулярности медиан \(AM\) и \(BN\) выражается через скалярное произведение соответствующих векторов:
\(\overrightarrow{AM} \cdot \overrightarrow{BN} = 0\), где
\(\overrightarrow{AM} = \left(\frac{x + 9}{2}; \frac{y}{2}\right)\),
\(\overrightarrow{BN} = \left(\frac{9}{2} — x; -y\right)\).
Раскрывая скалярное произведение, получаем уравнение:
\(\left(\frac{x + 9}{2}\right)\left(\frac{9}{2} — x\right) + \left(\frac{y}{2}\right)(-y) = 0\).
После преобразований это уравнение принимает вид:
\(2x^2 + 9x + 2y^2 — 81 = 0\).
Дополнительное уравнение возникает из того, что точка \(B\) находится на расстоянии \(12\) см от точки \(C\):
\((x — 9)^2 + y^2 = 144\).
Решая систему из двух уравнений, исключаем \(y^2\) и находим \(x = -1\). Подстановка этого значения обратно в уравнения дает \(y = 2\sqrt{11}\).
Искомое расстояние между точками \(A\) и \(B\) вычисляется по формуле расстояния между двумя точками:
\(AB = \sqrt{(-1 — 0)^2 + (2\sqrt{11} — 0)^2} = 3\sqrt{5}\) см.
Таким образом, длина стороны \(AB\) равна \(3\sqrt{5}\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!