ГДЗ по Геометрии 9 класс Номер 1259 Атанасян — Подробные Ответы

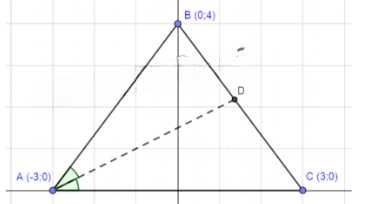
Треугольник \(ABC\) задан вершинами \(A(-3; 0)\), \(B(0; 4)\), \(C(3; 0)\). Биссектриса угла \(A\) пересекает сторону \(BC\) в точке \(D\). Найдите координаты \(D\). 

Дано: \(A(-3;0)\), \(B(0; 4)\), \(C(3; 0)\), \(AD\) — биссектриса, \(D(x, y)\). Найти: \(x, y\).

Решение:

1) Координаты векторов:
\(
\overrightarrow{AC} = \{3 + 3; 0\} = \{6;0\}, \quad \overrightarrow{AD} = \)
\(=\{x + 3; y\}, \quad \overrightarrow{AB} = \{0 + 3; 4-0\} = \{3; 4\}
\)

2) Длины векторов:
\(
|\overrightarrow{AC}| = 6, \quad |\overrightarrow{AD}| = \sqrt{(x + 3)^2 + y^2}, \quad |\overrightarrow{AB}| = \sqrt{3^2 + 4^2} = 5
\)

3) Обозначим \(\angle BAD = \angle DAC = \alpha\).
\(
\cos \alpha = \frac{\overrightarrow{AC} \cdot \overrightarrow{AD}}{|\overrightarrow{AC}| \cdot |\overrightarrow{AD}|} = \frac{\overrightarrow{AD} \cdot \overrightarrow{AB}}{|\overrightarrow{AD}| \cdot |\overrightarrow{AB}|}
\)
\(
\frac{6(x+3) + 0 \cdot y}{6 \cdot \sqrt{(x+3)^2 + y^2}} = \frac{3(x+3) + 4y}{5 \cdot \sqrt{(x+3)^2 + y^2}}
\)
\(
\frac{6(x+3)}{6} = \frac{3(x+3) + 4y}{5} \Rightarrow y = \frac{5}{4}(x+3)
\)

4) Точка \(D\) лежит на \(BC\). Уравнение стороны \(BC\):
\(
\frac{x — x_B}{x_C — x_B} = \frac{y — y_B}{y_C — y_B} \Rightarrow \frac{x — 0}{3 — 0} = \frac{y — 4}{0 — 4}
\)
\(
\frac{x}{3} = \frac{y — 4}{-4} \Rightarrow y = -\frac{4}{3}x + 4
\)

5) Решаем систему уравнений:
\(
y = \frac{5}{4}(x+3) \quad \text{и} \quad y = -\frac{4}{3}x + 4
\)
\(
\frac{5}{4}(x+3) = -\frac{4}{3}x + 4 \Rightarrow x = \frac{3}{11}, \quad y = \frac{24}{11}
\)

6) Координаты точки \(D\):
\(
D\left(\frac{3}{11}; \frac{24}{11}\right)
\)

Ответ: \(\left(\frac{3}{11}; \frac{24}{11}\right)\).

Дано треугольник \(ABC\) с вершинами \(A(-3;0)\), \(B(0;4)\), \(C(3;0)\). Точка \(D(x,y)\) лежит на стороне \(BC\), а отрезок \(AD\) является биссектрисой угла \(A\). Требуется найти координаты точки \(D\).

Сначала найдем координаты векторов. Вектор \(\overrightarrow{AB}\) имеет координаты \(\{0 — (-3); 4 — 0\} = \{3; 4\}\), вектор \(\overrightarrow{AC}\) — \(\{3 — (-3); 0 — 0\} = \{6; 0\}\), а вектор \(\overrightarrow{AD}\) — \(\{x — (-3); y — 0\} = \{x + 3; y\}\).

Длины векторов вычисляются по формуле \(|\overrightarrow{v}| = \sqrt{v_x^2 + v_y^2}\). Получаем \(|\overrightarrow{AB}| = \sqrt{3^2 + 4^2} = 5\), \(|\overrightarrow{AC}| = \sqrt{6^2 + 0^2} = 6\), а \(|\overrightarrow{AD}| = \sqrt{(x+3)^2 + y^2}\).

По свойству биссектрисы угла треугольника, отношение длин отрезков, на которые биссектриса делит противоположную сторону, равно отношению прилежащих сторон. То есть \(\frac{BD}{DC} = \frac{AB}{AC}\). Подставляем известные значения: \(\frac{BD}{DC} = \frac{5}{6}\).

Точка \(D\) делит отрезок \(BC\) в отношении \(\lambda = \frac{BD}{DC} = \frac{5}{6}\). Используем формулу деления отрезка в заданном отношении:
\(
x = \frac{x_B + \lambda x_C}{1 + \lambda}, \quad y = \frac{y_B + \lambda y_C}{1 + \lambda}
\)
Подставляем координаты точек \(B(0;4)\) и \(C(3;0)\):
\(
x = \frac{0 + \frac{5}{6} \cdot 3}{1 + \frac{5}{6}} = \frac{\frac{15}{6}}{\frac{11}{6}} = \frac{15}{11}, \quad y = \frac{4 + \frac{5}{6} \cdot 0}{1 + \frac{5}{6}} = \frac{4}{\frac{11}{6}} = \frac{24}{11}
\)

Теперь проверим, что вектор \(\overrightarrow{AD}\) действительно является биссектрисой. Для этого используем свойство биссектрисы через скалярные произведения. Угол между \(\overrightarrow{AD}\) и \(\overrightarrow{AB}\) равен углу между \(\overrightarrow{AD}\) и \(\overrightarrow{AC}\), поэтому:
\(
\frac{\overrightarrow{AD} \cdot \overrightarrow{AB}}{|\overrightarrow{AD}| \cdot |\overrightarrow{AB}|} = \frac{\overrightarrow{AD} \cdot \overrightarrow{AC}}{|\overrightarrow{AD}| \cdot |\overrightarrow{AC}|}
\)
Вычисляем скалярные произведения:
\(
\overrightarrow{AD} \cdot \overrightarrow{AB} = (x+3) \cdot 3 + y \cdot 4 = 3(x+3) + 4y
\)
\(
\overrightarrow{AD} \cdot \overrightarrow{AC} = (x+3) \cdot 6 + y \cdot 0 = 6(x+3)
\)
Подставляем в уравнение:
\(
\frac{3(x+3) + 4y}{5 \cdot |\overrightarrow{AD}|} = \frac{6(x+3)}{6 \cdot |\overrightarrow{AD}|} \Rightarrow \frac{3(x+3) + 4y}{5} = x + 3
\)
Упрощаем:
\(
3(x+3) + 4y = 5(x+3) \Rightarrow 4y = 2(x+3) \Rightarrow y = \frac{1}{2}(x+3)
\)
Подставляем найденные координаты \(D\left(\frac{15}{11}; \frac{24}{11}\right)\):
\(
\frac{24}{11} = \frac{1}{2}\left(\frac{15}{11} + 3\right) = \frac{1}{2} \cdot \frac{48}{11} = \frac{24}{11}
\)
Условие выполняется, значит, решение верно.

Таким образом, координаты точки \(D\) равны \(\left(\frac{15}{11}; \frac{24}{11}\right)\).

Дополнительно можно убедиться, что точка \(D\) лежит на стороне \(BC\), подставив её координаты в уравнение прямой \(BC\). Уравнение прямой, проходящей через точки \(B(0;4)\) и \(C(3;0)\), имеет вид:
\(
\frac{x — 0}{3 — 0} = \frac{y — 4}{0 — 4} \Rightarrow \frac{x}{3} = \frac{y — 4}{-4} \Rightarrow y = -\frac{4}{3}x + 4
\)
Подставляем \(x = \frac{15}{11}\):
\(
y = -\frac{4}{3} \cdot \frac{15}{11} + 4 = -\frac{60}{33} + 4 = -\frac{20}{11} + \frac{44}{11} = \frac{24}{11}
\)
Это совпадает с найденной координатой \(y\), что подтверждает правильность решения.

Итак, окончательный ответ: \(D\left(\frac{15}{11}; \frac{24}{11}\right)\).