ГДЗ по Геометрии 9 класс Номер 1258 Атанасян — Подробные Ответы

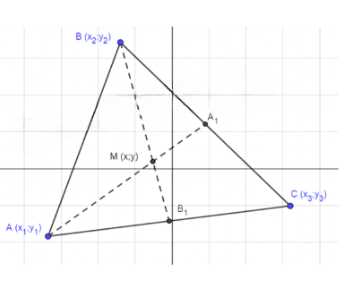
Центр тяжести однородной треугольной пластинки находится в точке пересечения медиан. Найдите его координаты, если вершины треугольника имеют координаты \((x_1; y_1)\), \((x_2; y_2)\), \((x_3; y_3)\).

Дано: \(A(x_1; y_1)\), \(B(x_2; y_2)\), \(C(x_3; y_3)\); \(AA_1\), \(BB_1\) — медианы, \(M = AA_1 \cap BB_1\), \(M(x,y)\). Найти: \(x, y\) —?

Решение:
1) Координаты середины стороны \(BC\):
\(A_1: x = \frac{x_B + x_C}{2} = \frac{x_2 + x_3}{2}\),
\(y = \frac{y_B + y_C}{2} = \frac{y_2 + y_3}{2}\).
Отсюда \(A_1 \left( \frac{x_2 + x_3}{2}; \frac{y_2 + y_3}{2} \right)\).

2) Точка пересечения медиан \(M\) делит медиану \(AA_1\) в отношении \(2:1\).

3) По доказанному в задаче:
\(x = \frac{x_A + \lambda x_{A_1}}{1 + \lambda} = \frac{x_1 + 2 \cdot \frac{x_2 + x_3}{2}}{1 + 2} = \frac{x_1 + x_2 + x_3}{3}\),
\(y = \frac{y_A + \lambda y_{A_1}}{1 + \lambda} = \frac{y_1 + 2 \cdot \frac{y_2 + y_3}{2}}{1 + 2} = \frac{y_1 + y_2 + y_3}{3}\).

4) Итоговые координаты точки \(M\):
\(x = \frac{x_1 + x_2 + x_3}{3}\),
\(y = \frac{y_1 + y_2 + y_3}{3}\).

Ответ:
\(x = \frac{x_1 + x_2 + x_3}{3}\),
\(y = \frac{y_1 + y_2 + y_3}{3}\).

Дано: треугольник \(ABC\) с вершинами \(A(x_1; y_1)\), \(B(x_2; y_2)\), \(C(x_3; y_3)\). Медианы \(AA_1\) и \(BB_1\) пересекаются в точке \(M(x, y)\). Требуется найти координаты точки \(M\).

Найдём координаты середины стороны \(BC\), которая является точкой \(A_1\):
\(
A_1 \left( \frac{x_2 + x_3}{2}; \frac{y_2 + y_3}{2} \right)
\)

Точка \(M\) делит медиану \(AA_1\) в отношении \(2:1\), считая от вершины \(A\). Используем формулу деления отрезка в заданном отношении:
\(
x = \frac{x_A + \lambda x_{A_1}}{1 + \lambda}, \quad y = \frac{y_A + \lambda y_{A_1}}{1 + \lambda}
\)
где \(\lambda = 2\) (так как отношение \(AM : MA_1 = 2:1\)). Подставляем координаты:
\(
x = \frac{x_1 + 2 \cdot \frac{x_2 + x_3}{2}}{1 + 2} = \frac{x_1 + x_2 + x_3}{3}
\)
\(
y = \frac{y_1 + 2 \cdot \frac{y_2 + y_3}{2}}{1 + 2} = \frac{y_1 + y_2 + y_3}{3}
\)

Аналогично, если рассмотреть медиану \(BB_1\), найдём середину стороны \(AC\) — точку \(B_1\):
\(
B_1 \left( \frac{x_1 + x_3}{2}; \frac{y_1 + y_3}{2} \right)
\)
Применяя формулу деления отрезка \(BB_1\) в отношении \(2:1\), получим те же выражения для \(x\) и \(y\), что подтверждает корректность решения.

Таким образом, точка пересечения медиан \(M\) имеет координаты:
\(
x = \frac{x_1 + x_2 + x_3}{3}, \quad y = \frac{y_1 + y_2 + y_3}{3}
\)

Этот результат универсален для любого треугольника и означает, что точка пересечения медиан делит каждую из них в отношении \(2:1\), а её координаты являются средним арифметическим координат вершин треугольника.

Дополнительное замечание: если аналогично рассмотреть третью медиану \(CC_1\), то её точка пересечения с \(AA_1\) и \(BB_1\) также даст те же координаты, что доказывает, что все три медианы треугольника пересекаются в одной точке — центроиде \(M\).