ГДЗ по Геометрии 9 класс Номер 1257 Атанасян — Подробные Ответы

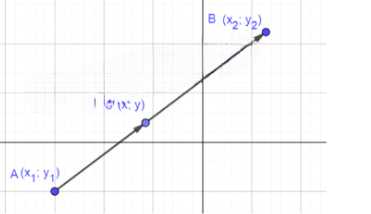
Даны точки \(A(x_1; y_1)\) и \(B(x_2; y_2)\). Найдите координаты \((x; y)\) точки \(C\), делящей отрезок \(AB\) в отношении \(\lambda\) (т. е. \(AC : CB = \lambda\)), по формулам \(x = \frac{\lambda x_2 + x_1}{1 + \lambda}\), \(y = \frac{\lambda y_2 + y_1}{1 + \lambda}\).

Дано четырёхугольник \(ABCD\) с координатами вершин \(A(x_1; y_1)\), \(B(x_2; y_2)\), \(C(x_3; y_3)\), \(D(x_4; y_4)\). Для параллелограмма выполняется условие: \((x_1 + x_3 = x_2 + x_4)\) и \((y_1 + y_3 = y_2 + y_4)\).

Доказательство необходимого условия: из равенства \((x_1 + x_3 = x_2 + x_4)\) следует \((x_2 — x_1 = x_3 — x_4)\). Вектор \(\overrightarrow{AB}\) имеет координаты \((x_2 — x_1; y_2 — y_1)\). Аналогично из \((y_1 + y_3 = y_2 + y_4)\) получаем \((y_2 — y_1 = y_3 — y_4)\). Вектор \(\overrightarrow{DC}\) равен \((x_3 — x_4; y_3 — y_4)\). Поскольку \(\overrightarrow{AB} = \overrightarrow{DC}\), четырёхугольник \(ABCD\) является параллелограммом.

Для достаточного условия: если \(ABCD\) — параллелограмм, то векторы \(\overrightarrow{AB}\) и \(\overrightarrow{DC}\) равны: \(\overrightarrow{AB} = \overrightarrow{DC}\). Отсюда следуют равенства \((x_2 — x_1 = x_3 — x_4)\) и \((y_2 — y_1 = y_3 — y_4)\), что эквивалентно исходным условиям \((x_1 + x_3 = x_2 + x_4)\) и \((y_1 + y_3 = y_2 + y_4)\).

Таким образом, равенство сумм соответствующих координат противоположных вершин является необходимым и достаточным условием для того, чтобы четырёхугольник был параллелограммом.

Рассмотрим четырёхугольник \(ABCD\) с вершинами в точках \(A(x_1; y_1)\), \(B(x_2; y_2)\), \(C(x_3; y_3)\) и \(D(x_4; y_4)\).

Для того чтобы этот четырёхугольник был параллелограммом, необходимо и достаточно выполнение следующих условий:

1. Суммы координат противоположных вершин должны быть равны:
\(x_1 + x_3 = x_2 + x_4\)
\(y_1 + y_3 = y_2 + y_4\)

2. Векторы, образованные сторонами \(AB\) и \(DC\), должны быть равны:
\(\overrightarrow{AB} = (x_2 — x_1; y_2 — y_1)\)
\(\overrightarrow{DC} = (x_3 — x_4; y_3 — y_4)\)
Условие \(\overrightarrow{AB} = \overrightarrow{DC}\) эквивалентно системе:
\(x_2 — x_1 = x_3 — x_4\)
\(y_2 — y_1 = y_3 — y_4\)

3. Средние точки диагоналей должны совпадать:
\(\left(\frac{x_1 + x_3}{2}; \frac{y_1 + y_3}{2}\right) = \left(\frac{x_2 + x_4}{2}; \frac{y_2 + y_4}{2}\right)\)

Доказательство необходимости: если \(ABCD\) — параллелограмм, то противоположные стороны равны и параллельны, что приводит к равенству соответствующих векторов и сумм координат.

Доказательство достаточности: если суммы координат противоположных вершин равны, то из этого следует равенство векторов \(\overrightarrow{AB}\) и \(\overrightarrow{DC}\), что гарантирует параллельность и равенство сторон \(AB\) и \(DC\). Аналогично доказывается для сторон \(AD\) и \(BC\).

Таким образом, данные условия являются полным критерием для определения параллелограмма по координатам его вершин.