ГДЗ по Геометрии 9 класс Номер 1256 Атанасян — Подробные Ответы

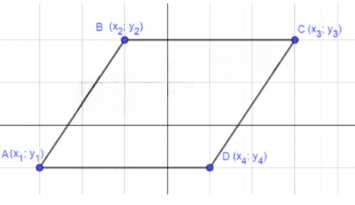
Четырёхугольник \(ABCD\) с вершинами \(A(x_1; y_1)\), \(B(x_2; y_2)\), \(C(x_3; y_3)\), \(D(x_4; y_4)\). Докажите, что он является параллелограммом тогда и только тогда, когда \(x_1 + x_3 = x_2 + x_4\) и \(y_1 + y_3 = y_2 + y_4\).

Дано четырехугольник ABCD с координатами вершин A(x₁; y₁), B(x₂; y₂), C(x₃; y₃), D(x₄; y₄). Для параллелограмма выполняется условие: (x₁ + x₃ = x₂ + x₄) и (y₁ + y₃ = y₂ + y₄).

Доказательство необходимого условия: из равенства (x₁ + x₃ = x₂ + x₄) следует (x₂ — x₁ = x₃ — x₄). Вектор AB имеет координаты (x₂ — x₁; y₂ — y₁). Аналогично из (y₁ + y₃ = y₂ + y₄) получаем (y₂ — y₁ = y₃ — y₄). Вектор DC равен (x₃ — x₄; y₃ — y₄). Поскольку (AB = DC), четырёхугольник ABCD является параллелограммом.

Для достаточного условия: если ABCD — параллелограмм, то векторы AB и DC равны: (AB = DC). Отсюда следуют равенства (x₂ — x₁ = x₃ — x₄) и (y₂ — y₁ = y₃ — y₄), что эквивалентно исходным условиям (x₁ + x₃ = x₂ + x₄) и (y₁ + y₃ = y₂ + y₄).

Таким образом, равенство сумм соответствующих координат противоположных вершин является необходимым и достаточным условием для того, чтобы четырёхугольник был параллелограммом.

Рассмотрим четырёхугольник \(ABCD\) с вершинами \(A(x_1; y_1)\), \(B(x_2; y_2)\), \(C(x_3; y_3)\), \(D(x_4; y_4)\). Для того чтобы этот четырёхугольник был параллелограммом, необходимо и достаточно выполнение следующих условий:
\((x_1 + x_3 = x_2 + x_4)\) и \((y_1 + y_3 = y_2 + y_4)\).

Доказательство необходимости: если \(ABCD\) — параллелограмм, то середины его диагоналей совпадают. Координаты середины диагонали \(AC\) вычисляются как \((\frac{x_1 + x_3}{2}, \frac{y_1 + y_3}{2})\), а середины диагонали \(BD\) — \((\frac{x_2 + x_4}{2}, \frac{y_2 + y_4}{2})\). Из равенства этих точек следует:
\((\frac{x_1 + x_3}{2} = \frac{x_2 + x_4}{2})\) и \((\frac{y_1 + y_3}{2} = \frac{y_2 + y_4}{2})\), что эквивалентно \((x_1 + x_3 = x_2 + x_4)\) и \((y_1 + y_3 = y_2 + y_4)\).

Доказательство достаточности: предположим, что выполняются равенства \((x_1 + x_3 = x_2 + x_4)\) и \((y_1 + y_3 = y_2 + y_4)\). Рассмотрим векторы \(\overrightarrow{AB} = (x_2 — x_1, y_2 — y_1)\) и \(\overrightarrow{DC} = (x_3 — x_4, y_3 — y_4)\). Из условия \((x_1 + x_3 = x_2 + x_4)\) следует \((x_2 — x_1 = x_3 — x_4)\), а из \((y_1 + y_3 = y_2 + y_4)\) — \((y_2 — y_1 = y_3 — y_4)\). Таким образом, \(\overrightarrow{AB} = \overrightarrow{DC}\), что означает равенство и параллельность сторон \(AB\) и \(DC\).

Аналогично, векторы \(\overrightarrow{AD} = (x_4 — x_1, y_4 — y_1)\) и \(\overrightarrow{BC} = (x_3 — x_2, y_3 — y_2)\). Из тех же условий получаем \((x_4 — x_1 = x_3 — x_2)\) и \((y_4 — y_1 = y_3 — y_2)\), откуда \(\overrightarrow{AD} = \overrightarrow{BC}\), что доказывает равенство и параллельность сторон \(AD\) и \(BC\).

Таким образом, если выполняются условия \((x_1 + x_3 = x_2 + x_4)\) и \((y_1 + y_3 = y_2 + y_4)\), то \(ABCD\) — параллелограмм. Обратно, если \(ABCD\) — параллелограмм, то эти условия выполняются. Это означает, что данные равенства являются необходимыми и достаточными условиями для того, чтобы четырёхугольник был параллелограммом.