Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1251 Атанасян — Подробные Ответы
Равнобедренный треугольник, боковая сторона которого равна m, а угол при основании равен ϕ, вращается вокруг основания. Найдите площадь поверхности тела, полученного при этом вращении.
1. Радиус основания конусов:
\( r = m \cdot \sin \phi \)
2. Площадь поверхности:
\( S_{\text{пов}} = 2\pi r l = 2\pi \cdot m \cdot \sin \phi \cdot m = 2\pi m^2 \sin \phi \)
3. Ответ:
\( S_{\text{пов}} = 2\pi m^2 \sin \phi \)
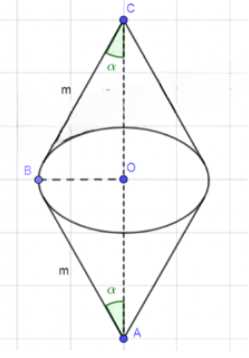
Дано равнобедренный треугольник \(\Delta ABC\) с боковыми сторонами \(AB = BC = m\) и углами при основании \(\angle A = \angle C = \phi\). Требуется найти площадь поверхности тела, полученного вращением этого треугольника вокруг его основания \(AC\).
При вращении \(\Delta ABC\) вокруг стороны \(AC\) образуется тело, состоящее из двух одинаковых конусов, соединенных основаниями.
Найдем параметры конусов:
Высота каждого конуса равна расстоянию от вершины \(B\) до основания \(AC\), то есть высоте треугольника \(h = OB\). Так как треугольник равнобедренный, то \(OB\) является одновременно медианой, биссектрисой и высотой.
Радиус основания конусов \(r\) равен половине стороны \(AC\), но его можно выразить через боковую сторону \(m\) и угол \(\phi\):
\( r = m \cdot \sin \phi \)
Высота конуса \(h\) вычисляется по теореме Пифагора:
\( h = \sqrt{m^2 — r^2} = \sqrt{m^2 — (m \sin \phi)^2} = m \cos \phi \)
Площадь боковой поверхности одного конуса:
\( S_{\text{бок}} = \pi r l \)
где \(l\) — образующая конуса, равная \(m\).
Таким образом, площадь поверхности двух конусов:
\( S_{\text{пов}} = 2 \cdot \pi r l = 2 \pi \cdot m \sin \phi \cdot m = 2 \pi m^2 \sin \phi \)
Итоговый ответ:
\( S_{\text{пов}} = 2 \pi m^2 \sin \phi \)
Дополнительно можно проверить, что если \(\phi = 90^\circ\), то \(\sin \phi = 1\), и площадь поверхности становится \(2 \pi m^2\), что соответствует площади цилиндра высотой \(m\) и радиусом \(m\), что логично, так как при \(\phi = 90^\circ\) треугольник становится прямоугольным, и вращение дает цилиндр.
Если требуется найти полную площадь поверхности (включая основания), то нужно добавить площадь двух кругов:
\( S_{\text{полн}} = 2 \pi m^2 \sin \phi + 2 \pi r^2 = 2 \pi m^2 \sin \phi + 2 \pi m^2 \sin^2 \phi \)
Но в исходной задаче, судя по записи, требуется только боковая поверхность.
Таким образом, окончательный ответ остается:
\( S_{\text{пов}} = 2 \pi m^2 \sin \phi \)
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.