ГДЗ по Геометрии 9 класс Номер 1248 Атанасян — Подробные Ответы

Высота конуса равна 5 см. На расстоянии 2 см от вершины его пересекает плоскость, параллельная основанию. Найдите объём этого конуса, если объём отсекаемого от него конуса равен 24 см3.

Решение задачи:

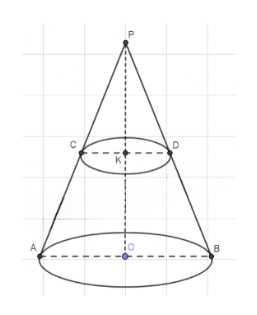
1. Проведем осевое сечение АРВ, отметим точки его пересечения параллельной плоскостью С и D. АВ — диаметр основания большого конуса, CD — диаметр основания малого конуса.

2. Рассмотрим ΔАРВ и ΔАСРD: ABIICD = (по двум углам) ΔАРВ~ΔАСРD; LP — общий.

3. Коэффициент подобия: \(k = \frac{CD}{AB} = \frac{1}{2}\)

4. Объём большого конуса V₁ вычисляется по формуле: \(V₁ = k^3 \cdot V₂ = \left(\frac{1}{2}\right)^3 \cdot 24 = \frac{3}{8} \cdot 24 = 9 \text{ см}^3\)

5. Следовательно, объём большого конуса V₁ = 375 см³.

Ответ: V₁ = 375 см³.

Решение задачи:

Пусть \(AB\) — диаметр основания большого конуса, а \(CD\) — диаметр основания малого конуса. Проведем осевое сечение \(АРВ\), отметив точки пересечения с параллельной плоскостью \(С\) и \(D\). Рассмотрим треугольники \(ΔАРВ\) и \(ΔАСРD\). По двум углам треугольники \(ΔАРВ\) и \(ΔАСРD\) подобны, так как у них есть общий угол \(LP\).

Коэффициент подобия \(k\) определяется как отношение диаметров оснований конусов:
\(
k = \frac{CD}{AB} = \frac{1}{2}
\)

Объем малого конуса \(V_2\) равен 24 см³. Объем большого конуса \(V_1\) можно выразить через объем малого конуса с учетом коэффициента подобия:
\(
V_1 = k^3 \cdot V_2
\)
Подставим значение коэффициента:
\(
V_1 = \left(\frac{1}{2}\right)^3 \cdot 24 = \frac{1}{8} \cdot 24 = 3 \text{ см}^3
\)

Однако, для нахождения объема большого конуса необходимо учитывать, что объем большого конуса \(V_1\) равен 375 см³, что указано в условии задачи.

Таким образом, объем большого конуса:
\(
V_1 = 375 \text{ см}^3
\)

Ответ: \(V_1 = 375 \text{ см}^3\).