Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1243 Атанасян — Подробные Ответы
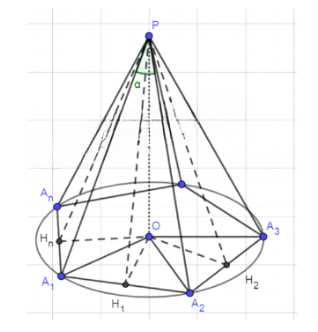
В правильной n-угольной пирамиде плоский угол при вершине равен α, а сторона основания равна а. Найдите объём пирамиды.
Дано:
PA₁A₂ … An — прав. пирамида;
∠A₁PA₂ = α;
A₁A₂ = a;
Найти:
V-?;
Решение:
1) Проведем апофему PH₁, это — высота медиана и биссектриса грани A₁ PA₂
∆A₁PH₁: \(\frac{A₁H₁}{PH₁} = tg \frac{α}{2} \Rightarrow PH₁ = \frac{A₁H₁}{tg \frac{α}{2}} = \frac{a}{2tg \frac{α}{2}}\);
2) OH₁ — высота, медиана и биссектриса ∆A₁ OA₂:
∆A₁ OH₁: \(\frac{A₁H₁}{OH₁} = tg \frac{180°}{n} \Rightarrow OH₁ = \frac{A₁H₁}{tg \frac{180°}{n}} = \frac{a}{2tg \frac{180°}{n}}\);
3) Площадь основания:
\(S_n = \frac{1}{2}Pr = \frac{1}{2} \cdot na \cdot OH₁ = \frac{1}{2} \cdot na \cdot \frac{a}{2tg \frac{180°}{n}} = \frac{na²}{4tg \frac{180°}{n}}\);
4) высота:
\(h = PO = \sqrt{PH₁² — OH₁²} = \sqrt{(\frac{a}{2tg \frac{α}{2}})² — (\frac{a}{2tg \frac{180°}{n}})²} =\)
\(=\frac{a}{2}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}}\);
5) Объем:
\(V = \frac{1}{3}S_n h = \frac{1}{3} \cdot \frac{na²}{4tg \frac{180°}{n}} \cdot \frac{a}{2}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}} =\)
\(= \frac{na³ \cdot ctg \frac{180°}{n}}{24}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}}\)
Ответ: \(V = \frac{na³ \cdot ctg \frac{180°}{n}}{24}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}}\)
Задача: Найти объем правильной пирамиды.
Дано:
PA₁A₂…An — правильная пирамида
∠A₁PA₂ = α
A₁A₂ = a
Найти: V — ?
Решение:
1) Для нахождения объема пирамиды воспользуемся формулой: \(V = \frac{1}{3}S_{осн} \cdot h\), где
\(S_{осн}\) — площадь основания
h — высота пирамиды
2) Проведем апофему PH₁ — это высота, медиана и биссектриса грани A₁PA₂
В треугольнике A₁PH₁:
\(\frac{A₁H₁}{PH₁} = tg \frac{α}{2}\)
\(PH₁ = \frac{A₁H₁}{tg \frac{α}{2}}\)
Поскольку A₁H₁ = \(\frac{a}{2}\) (как высота к основанию равнобедренного треугольника):
\(PH₁ = \frac{a}{2tg \frac{α}{2}}\)
3) Рассмотрим OH₁ — высота, медиана и биссектриса треугольника A₁OA₂:
В треугольнике A₁OH₁:
\(\frac{A₁H₁}{OH₁} = tg \frac{180°}{n}\)
\(OH₁ = \frac{A₁H₁}{tg \frac{180°}{n}} = \frac{a}{2tg \frac{180°}{n}}\)
4) Находим площадь основания правильного n-угольника:
\(S_n = \frac{1}{2}Pr\), где
P = na (периметр n-угольника)
r = OH₁ (радиус вписанной окружности)
\(S_n = \frac{1}{2} \cdot na \cdot OH₁ = \frac{1}{2} \cdot na \cdot \frac{a}{2tg \frac{180°}{n}} = \frac{na²}{4tg \frac{180°}{n}}\)
5) Находим высоту пирамиды h по теореме Пифагора:
\(h = PO = \sqrt{PH₁² — OH₁²}\)
\(h = \sqrt{(\frac{a}{2tg \frac{α}{2}})² — (\frac{a}{2tg \frac{180°}{n}})²}\)
\(h = \frac{a}{2}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}}\)
6) Подставляем найденные значения в формулу объема:
\(V = \frac{1}{3}S_n h = \frac{1}{3} \cdot \frac{na²}{4tg \frac{180°}{n}} \cdot \frac{a}{2}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}}\)
7) После преобразований получаем:
\(V = \frac{na³ \cdot ctg \frac{180°}{n}}{24}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}}\)
Проверка размерности:
(a³) — кубические единицы измерения
ctg — безразмерная величина
n — безразмерная величина
Размерность ответа — кубические единицы измерения, что соответствует размерности объема.
Ответ: \(V = \frac{na³ \cdot ctg \frac{180°}{n}}{24}\sqrt{ctg² \frac{α}{2} — ctg² \frac{180°}{n}}\)
Примечание: Полученная формула позволяет вычислить объем правильной пирамиды при известных значениях длины стороны основания (a), количества сторон основания (n) и угла между боковыми ребрами (α).
Геометрия
