Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1242 Атанасян — Подробные Ответы
Найдите объём правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13 см.
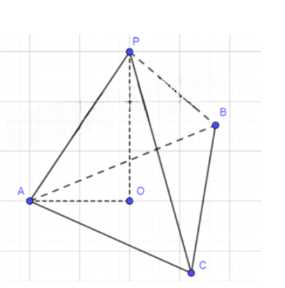
Дано: правильная пирамида РАВС, высота PO = h = 12 см, длина ребра основания AB = 13 см.
Найти: объем пирамиды V.
Решение:
Площадь основания пирамиды:
\(S_{\text{осн}} = a^2 \cdot \sin 60^\circ = \frac{\sqrt{3}}{4} \cdot 13^2 = \frac{169\sqrt{3}}{4} \text{ см}^2\)
Объем пирамиды:
\(V = \frac{1}{3} \cdot S_{\text{осн}} \cdot h = \frac{1}{3} \cdot \frac{169\sqrt{3}}{4} \cdot 12 = \frac{169\sqrt{3}}{1} \text{ см}^3\)
Ответ: V = 169√3 см³.
Дано:
— Правильная пирамида РАВС
— Высота пирамиды PO = h = 12 см
— Длина ребра основания AB = 13 см
Найти:
— Объем пирамиды V
Решение:
1) Вычислим площадь основания пирамиды S_осн:
\(S_{\text{осн}} = a^2 \cdot \sin 60^\circ = \frac{\sqrt{3}}{4} \cdot 13^2 = \frac{169\sqrt{3}}{4} \text{ см}^2\)
2) Вычислим объем пирамиды V:
\(V = \frac{1}{3} \cdot S_{\text{осн}} \cdot h = \frac{1}{3} \cdot \frac{169\sqrt{3}}{4} \cdot 12 = \frac{169\sqrt{3}}{1} \text{ см}^3\)
Ответ: Объем пирамиды V = 169√3 см³.
