Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1241 Атанасян — Подробные Ответы
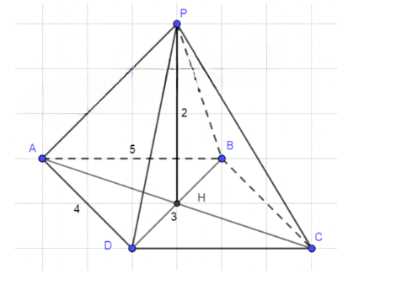
Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь поверхности пирамиды, т. е. сумму площадей всех её граней.
Дано:
\( PABCD \) — пирамида;
\( ABCD \) — параллелограмм;
\( AB = 5 \, \text{м} \);
\( AD = 4 \, \text{м} \);
\( BD = 3 \, \text{м} \);
\( H \in AC \cap BD \);
\( PH \) — высота;
\( PH = 2 \, \text{м} \);
Найти: \( S_{\text{поверхности}} \) — ?
Решение:
1) \(\triangle ADB\) — египетский треугольник. \(\angle ADB = 90^\circ\);
2) \(S_{ABCD} = 2S_{ADB} = 2 \cdot \frac{1}{2} \cdot AD \cdot BD = 4 \cdot 3 = 12 \, \text{м}^2\);
3) \(AD \perp DBP \Rightarrow AD \perp PD \Rightarrow \angle ADP = 90^\circ\);
4) \(DP = \sqrt{DH^2 + PH^2} = \sqrt{\left(\frac{3}{2}\right)^2 + 2^2} = \sqrt{6.25} = 2.5 \, \text{м}\);
5) \(AP = \sqrt{AD^2 + DP^2} = \sqrt{4^2 + 2.2^2} = \sqrt{22.25} = \sqrt{\frac{89}{4}} = \frac{\sqrt{89}}{2} \, \text{м}\);
6) \(AH = HC\)
\( PH \) — общая сторона, значит \(\triangle APH = \triangle CPH\) (по \(\angle PHA = \angle PHC\) первому признаку), отсюда \(AP = CP\); \(BH = HD\)
7) \(PH\) — общая сторона, значит \(\triangle ABPH = \triangle DPH\) (по \(\angle PHB = \angle PHD\) первому признаку), отсюда \(BP = DP\);
8) Получаем:
\(\triangle APD = \triangle CPB\) — по трём сторонам и \(\triangle ABP = \triangle CPD\) — по трём сторонам
9) \(S_{APD} = \frac{1}{2} AD \cdot DP = \frac{1}{2} \cdot 4 \cdot 2.5 = 5 \, \text{м}^2\);
10) В \(\triangle APB\): \(\cos \angle PAB = \frac{AP^2 + AB^2 — BP^2}{2AP \cdot AB} = \frac{\frac{89}{4} + 25 — 25}{2 \cdot \frac{\sqrt{89}}{2} \cdot 5} = \frac{41}{5\sqrt{89}}\);
11) \(\sin \angle PAB = \sqrt{1 — \cos^2 \angle PAB} = \sqrt{1 — \frac{41^2}{52 \cdot 89}} = \frac{\sqrt{544}}{5\sqrt{89}} = \frac{4\sqrt{34}}{5\sqrt{89}}\);
12) \(S_{APB} = \frac{1}{2} AP \cdot AB \cdot \sin \angle PAB = \frac{1}{2} \cdot \frac{\sqrt{89}}{2} \cdot 5 \cdot \frac{4\sqrt{34}}{5\sqrt{89}} = \sqrt{34} \, \text{м}^2\).
Площадь поверхности:
\( S_{\text{полн}} = S_{ABCD} + 2S_{APD} + 2S_{APB} = 12 + 2 \cdot 5 + 2 \cdot \sqrt{34} = 2(11 + \sqrt{34}) \, \text{м}^2 \) или около \( 33 \frac{2}{3} \, \text{м}^2 \);
Ответ: \( S_{\text{поверхности}} = 33 \frac{2}{3} \, \text{м}^2 \).
Дано:
\( PABCD \) — пирамида;
\( ABCD \) — параллелограмм;
\( AB = 5 \, \text{м} \);
\( AD = 4 \, \text{м} \);
\( BD = 3 \, \text{м} \);
\( H \in AC \cap BD \);
\( PH \) — высота;
\( PH = 2 \, \text{м} \);
Найти: \( S_{\text{поверхности}} \)
Решение:
1) Рассмотрим \(\triangle ADB\). Это египетский треугольник, так как \(\angle ADB = 90^\circ\).
2) Площадь параллелограмма \(ABCD\) равна удвоенной площади \(\triangle ADB\):
\( S_{ABCD} = 2S_{ADB} = 2 \cdot \frac{1}{2} \cdot AD \cdot BD = 4 \cdot 3 = 12 \, \text{м}^2 \)
3) Из условия \(AD \perp DBP\) следует, что \(AD \perp PD\), значит \(\angle ADP = 90^\circ\).
4) Найдем \(DP\) по теореме Пифагора в \(\triangle DHP\):
\( DP = \sqrt{DH^2 + PH^2} = \sqrt{\left(\frac{3}{2}\right)^2 + 2^2} = \sqrt{2.25 + 4} = \sqrt{6.25} = 2.5 \, \text{м} \)
5) Найдем \(AP\) по теореме Пифагора в \(\triangle ADP\):
\( AP = \sqrt{AD^2 + DP^2} = \sqrt{4^2 + 2.5^2} = \sqrt{16 + 6.25} = \sqrt{22.25} = \sqrt{\frac{89}{4}} = \frac{\sqrt{89}}{2} \, \text{м} \)
6) Так как \(AH = HC\) и \(PH\) — общая сторона, \(\triangle APH = \triangle CPH\) (по первому признаку равенства треугольников), отсюда \(AP = CP\) и \(BH = HD\).
7) Так как \(PH\) — общая сторона, \(\triangle ABPH = \triangle DPH\) (по первому признаку равенства треугольников), отсюда \(BP = DP\).
8) Получаем, что \(\triangle APD = \triangle CPB\) (по трём сторонам) и \(\triangle ABP = \triangle CPD\) (по трём сторонам).
9) Площадь \(\triangle APD\) равна:
\( S_{APD} = \frac{1}{2} \cdot AD \cdot DP = \frac{1}{2} \cdot 4 \cdot 2.5 = 5 \, \text{м}^2 \)
10) В \(\triangle APB\) найдем \(\cos \angle PAB\) по теореме косинусов:
\( \cos \angle PAB = \frac{AP^2 + AB^2 — BP^2}{2 \cdot AP \cdot AB} = \frac{\frac{89}{4} + 25 — 25}{2 \cdot \frac{\sqrt{89}}{2} \cdot 5} = \frac{41}{5\sqrt{89}} \)
11) Найдем \(\sin \angle PAB\) через \(\cos \angle PAB\):
\( \sin \angle PAB = \sqrt{1 — \cos^2 \angle PAB} = \sqrt{1 — \left(\frac{41}{5\sqrt{89}}\right)^2} = \frac{\sqrt{544}}{5\sqrt{89}} = \frac{4\sqrt{34}}{5\sqrt{89}} \)
12) Площадь \(\triangle APB\) равна:
\( S_{APB} = \frac{1}{2} \cdot AP \cdot AB \cdot \sin \angle PAB = \frac{1}{2} \cdot \frac{\sqrt{89}}{2} \cdot 5 \cdot \frac{4\sqrt{34}}{5\sqrt{89}} = \sqrt{34} \, \text{м}^2 \)
Площадь полной поверхности пирамиды:
\( S_{\text{полн}} = S_{ABCD} + 2S_{APD} + 2S_{APB} = 12 + 2 \cdot 5 + 2 \cdot \sqrt{34} = 2(11 + \sqrt{34}) \, \text{м}^2 \)
Приблизительно это равно \( 33 \frac{2}{3} \, \text{м}^2 \).
Ответ: \( S_{\text{поверхности}} = 33 \frac{2}{3} \, \text{м}^2 \).
Геометрия
