Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1240 Атанасян — Подробные Ответы
Изобразите тетраэдр DABC, отметьте точку K на ребре DC и точки M и N граней ABC и ACD. Постройте сечение тетраэдра плоскостью MNK.
Дано: \(ABCD\) — тетраэдр; \(K \in DC\); \(M \in ABC\); \(N \in ACD\); Построить: сечение \(MNK\);
Построение:
1) Точки \(N\) и \(K\) лежат на одной грани, построим луч \(KN\);
2) Отметим точку пересечения \(KN\) и \(AD\) — \(E\);
3) Построим луч \(CA\), отметим точку пересечения \(CA\) и \(KN\) — \(F\);
4) Проведем луч \(FM\), отметим точки пересечения луча и ребер тетраэдра \(G\) и \(H\);
5) Плоскость \(EGHK\) — искомая;
Для построения сечения тетраэдра \(ABCD\) плоскостью \(MNK\) следуем указанным шагам:
1. Изобразим тетраэдр \(ABCD\): нарисуйте четыре вершины \(A\), \(B\), \(C\), \(D\) и соедините их ребрами, чтобы получить тетраэдр.
2. Отметьте точки \(K\), \(M\), \(N\): точка \(K\) находится на ребре \(DC\), точка \(M\) находится на грани \(ABC\), точка \(N\) находится на грани \(ACD\).
3. Построение луча \(KN\): соедините точки \(K\) и \(N\) прямой линией, чтобы получить луч \(KN\).
4. Определение точки \(E\): найдите точку пересечения луча \(KN\) с ребром \(AD\). Это будет точка \(E\).
5. Построение луча \(CA\): проведите луч от точки \(C\) через точку \(A\).
6. Определение точки \(F\): найдите точку пересечения луча \(CA\) с лучом \(KN\). Это будет точка \(F\).
7. Построение луча \(FM\): проведите луч от точки \(F\) через точку \(M\).
8. Определение точек \(G\) и \(H\): найдите точки пересечения луча \(FM\) с ребрами тетраэдра. Обозначьте их как \(G\) и \(H\).
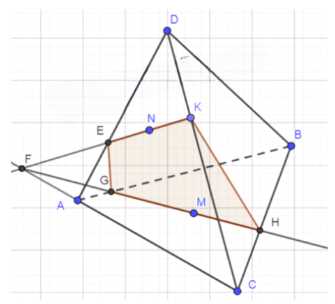
9. Построение искомой плоскости \(EGHK\): соедините точки \(E\), \(G\), \(H\), \(K\) для получения плоскости \(EGHK\), которая является искомым сечением.
Таким образом, вы получили сечение тетраэдра плоскостью, проходящей через точки \(M\), \(N\), \(K\). Это сечение представляет собой четырехугольник \(EGHK\).
Геометрия
