ГДЗ по Геометрии 9 класс Номер 1236 Атанасян — Подробные Ответы

Сумма площадей трёх граней прямоугольного параллелепипеда, имеющих общую вершину, равна 404 дм2, а его рёбра пропорциональны числам 3, 7 и 8. Найдите диагональ параллелепипеда.

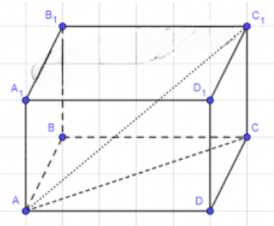
Дано: \(ABCDA_1B_1C_1D_1\) — прямоугольный параллелепипед; Найти: \(AC_1-\)?

Решение:

1) Обозначим: \(AB = DC = A_1B_1 = D_1C_1 = a\), \(AD = BC = A_1D_1 = B_1C_1 = b\), \(AA_1 = BB_1 = CC_1 = c\).

2) Соотношение сторон: \(c : a : b = 3 : 7 : 8\).

3) Пусть \(c = 3x\), \(a = 7x\), \(b = 8x\).

4) Сумма площадей: \(ac + ab + bc = 404\)

\(7 \cdot 3x + 7 \cdot 8x + 8x \cdot 3x = 404 \Rightarrow 101x^2 = 404 \Rightarrow x^2 = 4 \Rightarrow x = 2\)

\(a = 7x = 14\) (дм), \(b = 8x = 16\) (дм), \(c = 3x = 6\) (дм).

\(AC_1 = \sqrt{a^2 + b^2 + c^2} = \sqrt{14^2 + 16^2 + 6^2} = \sqrt{196 + 256 + 36} =\)
\(=\sqrt{488} = 2\sqrt{122}\) (дм).

Ответ: \(AC_1 = 2\sqrt{122}\) дм.

Дано: \(ABCDA_1B_1C_1D_1\) — прямоугольный параллелепипед. Найти: \(AC_1\).

Решение:

1) Обозначим стороны параллелепипеда:
— \(AB = DC = A_1B_1 = D_1C_1 = a\)
— \(AD = BC = A_1D_1 = B_1C_1 = b\)
— \(AA_1 = BB_1 = CC_1 = c\)

2) Дано соотношение сторон: \(c : a : b = 3 : 7 : 8\).

3) Пусть:
— \(c = 3x\)
— \(a = 7x\)
— \(b = 8x\)

4) Используем условие, что сумма площадей трех граней равна 404:
\(
ac + ab + bc = 404
\)

Подставим выражения для \(a\), \(b\), \(c\):
\(
(7x)(3x) + (7x)(8x) + (8x)(3x) = 404
\)

Упростим выражение:
\(
21x^2 + 56x^2 + 24x^2 = 404
\)

\(
101x^2 = 404
\)

Найдем \(x^2\):
\(
x^2 = \frac{404}{101} = 4
\)

\(
x = 2
\)

5) Найдем длины сторон:
— \(a = 7x = 7 \times 2 = 14\) дм
— \(b = 8x = 8 \times 2 = 16\) дм
— \(c = 3x = 3 \times 2 = 6\) дм

6) Найдем диагональ \(AC_1\) с помощью теоремы о трехмерной диагонали:
\(
AC_1 = \sqrt{a^2 + b^2 + c^2}
\)

Подставим найденные значения:
\(
AC_1 = \sqrt{14^2 + 16^2 + 6^2}
\)

\(
AC_1 = \sqrt{196 + 256 + 36}
\)

\(
AC_1 = \sqrt{488}
\)

Разложим подкоренное выражение на множители:
\(
AC_1 = \sqrt{4 \times 122} = 2\sqrt{122}
\)

Ответ: \(AC_1 = 2\sqrt{122}\) дм.