
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1235 Атанасян — Подробные Ответы
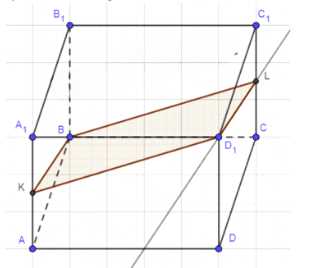
Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью BKL, где K — середина ребра AA1, а L — середина ребра СС1. Докажите, что построенное сечение — параллелограмм.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед; \(K\) — середина \(AA_1\); \(L\) — середина \(CC_1\).
Построить: сечение \(BKL\);
Построение:
1) Проведем отрезок \(BK\);
2) Так как \(ABA_1B_1 \parallel DD_1CC_1\), через точку \(L\) построим прямую, параллельную \(BK\);
3) Прямая проходит через точку \(D_1\);
4) Плоскость \(BKLD_1\) — искомая;
Доказать: \(BKLD_1\) — параллелограмм;
Доказательство:
1) \(ABCDA_1B_1C_1D_1\) — параллелепипед, следовательно: \(KD_1 \parallel BL\) и \(KB \parallel D_1L\);
2) Рассмотрим \(\triangle AKB\) и \(\triangle D_1LC_1\): \(KA = C_1L\) (по условию), \(AB = D_1C_1\) и \(\angle AKB = \angle D_1LC_1\) (по свойству параллелепипеда), значит \(\triangle AKB \cong \triangle D_1LC_1\). Отсюда \(KB = D_1L\).
3) \(KD_1 \parallel BL\); \(KB \parallel D_1L\) и \(KB = D_1L\), следовательно \(KBD_1L\) — параллелограмм, что и требовалось доказать.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед; \(K\) — середина \(AA_1\); \(L\) — середина \(CC_1\).
Построить: сечение \(BKL\).
Построение:
1. Проведем отрезок \(BK\).
2. Поскольку \(ABA_1B_1 \parallel DD_1CC_1\), через точку \(L\) строим прямую, параллельную \(BK\).
3. Прямая проходит через точку \(D_1\).
4. Образуется плоскость \(BKLD_1\), которая является искомой.
Доказательство, что \(BKLD_1\) — параллелограмм:
1. Поскольку \(ABCDA_1B_1C_1D_1\) — параллелепипед, следовательно, \(KD_1 \parallel BL\) и \(KB \parallel D_1L\).
2. Рассмотрим треугольники \(\triangle AKB\) и \(\triangle D_1LC_1\):
— \(KA = C_1L\) (по условию, так как \(K\) и \(L\) — середины),
— \(AB = D_1C_1\) (по свойству параллелепипеда),
— \(\angle AKB = \angle D_1LC_1\) (так как они соответствующие при параллельных прямых).
Следовательно, \(\triangle AKB \cong \triangle D_1LC_1\) по двум сторонам и углу между ними. Отсюда \(KB = D_1L\).
3. Поскольку \(KD_1 \parallel BL\), \(KB \parallel D_1L\) и \(KB = D_1L\), то \(KBD_1L\) является параллелограммом, что и требовалось доказать.
Таким образом, сечение \(BKL\) в параллелепипеде действительно образует параллелограмм.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!