
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1233 Атанасян — Подробные Ответы
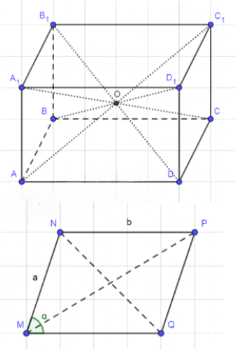
Докажите, что сумма квадратов четырёх диагоналей параллелепипеда равна сумме квадратов двенадцати его рёбер.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед;
Доказать: сумма квадратов диагоналей равна сумме квадратов ребер.
Доказательство:
Докажем лемму:
1) Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
2) Рассмотрим параллелограмм \(MNPQ\), \(\angle M = \alpha\), \(MN = PQ = a\), \(NP = MQ = b\).
3) По теореме косинусов:
\(NQ^2 = a^2 + b^2 — 2ab \cdot \cos \alpha\)
\(MP^2 = a^2 + b^2 — 2ab \cdot \cos(180^\circ — \alpha) = a^2 + b^2 + 2ab \cdot \cos \alpha\)
\(NQ^2 + MP^2 = 2a^2 + 2b^2 = MN^2 + NP^2 + PQ^2 + MQ^2\)
Лемма доказана.
3) Получаем для параллелограмма \(AA_1C_1C\):
\(AC^2 + A_1C^2 = AA^2 + A_1C^2 + CC^2 + AC^2\)
4) Для параллелограмма \(BB_1D_1D\):
\(BD^2 + B_1D^2 = BB^2 + B_1D^2 + DD^2 + BD^2\)
5) Для параллелограмма \(ABCD\):
\(AC^2 + BD^2 = AB^2 + BC^2 + CD^2 + AD^2\)
6) Аналогично — для параллелограмма \(A_1B_1C_1D_1\):
\(A_1C^2 + B_1D^2 = A_1B^2 + B_1C^2 + C_1D^2 + A_1D^2\)
7) Сумма квадратов всех четырех диагоналей:
\(AC^2 + A_1C^2 + BD^2 + B_1D^2 = AA^2 + A_1C^2 + CC^2 + \)
\(+ AC^2 + BB^2 + B_1D^2 + DD^2 + BD^2 =AA^2 + BB^2 + CC^2 + \)
\(+ DD^2 + (AC^2 + BD^2) + (A_1C^2 + B_1D^2) = AA^2 + BB^2 + \)
\(+ CC^2 + DD^2 + AB^2 + BC^2 + CD^2 + AD^2 + AB^2 + B_1C^2 + \)
\(+ C_1D^2 + A_1D^2\) равна сумме квадратов всех ребер.
Что и требовалось доказать.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед.
Необходимо доказать, что сумма квадратов диагоналей равна сумме квадратов всех ребер.
Доказательство:
1. Докажем лемму: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
2. Рассмотрим параллелограмм \(MNPQ\) с углом \(\angle M = \alpha\), где \(MN = PQ = a\) и \(NP = MQ = b\).
3. По теореме косинусов для диагоналей параллелограмма:
\(
NQ^2 = a^2 + b^2 — 2ab \cdot \cos \alpha
\)
\(
MP^2 = a^2 + b^2 — 2ab \cdot \cos(180^\circ — \alpha) = a^2 + b^2 + 2ab \cdot \cos \alpha
\)
4. Сложив полученные выражения, получаем:
\(
NQ^2 + MP^2 = 2a^2 + 2b^2 = MN^2 + NP^2 + PQ^2 + MQ^2
\)
Лемма доказана.
5. Рассмотрим параллелограммы в параллелепипеде:
Для параллелограмма \(AA_1C_1C\):
\(
AC^2 + A_1C^2 = AA^2 + A_1C^2 + CC^2 + AC^2
\)
Для параллелограмма \(BB_1D_1D\):
\(
BD^2 + B_1D^2 = BB^2 + B_1D^2 + DD^2 + BD^2
\)
Для параллелограмма \(ABCD\):
\(
AC^2 + BD^2 = AB^2 + BC^2 + CD^2 + AD^2
\)
Аналогично для параллелограмма \(A_1B_1C_1D_1\):
\(
A_1C^2 + B_1D^2 = A_1B^2 + B_1C^2 + C_1D^2 + A_1D^2
\)
6. Сумма квадратов всех четырех диагоналей параллелепипеда:
\(
AC^2 + A_1C^2 + BD^2 + B_1D^2 = AA^2 + A_1C^2 + CC^2 + AC^2 +\)
\(+ BB^2 + B_1D^2 + DD^2 + BD^2
\)
Это равно:
\(
AA^2 + BB^2 + CC^2 + DD^2 + (AC^2 + BD^2) + (A_1C^2 + B_1D^2)
\)
Переписываем с учетом диагоналей:
\(
AA^2 + BB^2 + CC^2 + DD^2 + AB^2 + \)
\(+ BC^2 + CD^2 + AD^2 + A_1B^2 + B_1C^2 + C_1D^2 + A_1D^2
\)
7. Таким образом, мы показали, что сумма квадратов всех четырех диагоналей равна сумме квадратов всех ребер параллелепипеда.
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!