
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1232 Атанасян — Подробные Ответы
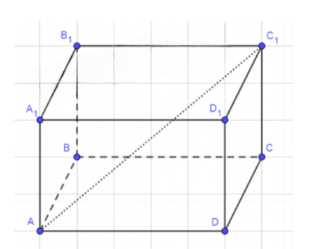
Докажите, что диагональ параллелепипеда меньше суммы трёх рёбер, имеющих общую вершину.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед;
Доказать: \(AC_1 < AB + AD + AA_1\);
Доказательство:
1) Из \(\Delta ACC_1\) по неравенству треугольника:
\(AC_1 < AC + CC_1\)
2) Из \(\Delta ABC\) по неравенству треугольника:
\(AC < AB + BC\)
3) Учитывая, что все грани параллелепипеда — параллелограммы, получаем:
\(AC_1 < AC + CC_1 < (AB + BC) = AD + AA_1\)
Это и требовалось доказать.
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед. Необходимо доказать, что \(AC_1 < AB + AD + AA_1\).
Доказательство:
1) Рассмотрим треугольник \(ACC_1\). По неравенству треугольника:
\[ AC_1 < AC + CC_1 \]
2) Рассмотрим треугольник \(ABC\). По неравенству треугольника:
\[ AC < AB + BC \]
3) Учитывая, что все грани параллелепипеда являются параллелограммами, можем сделать следующие выводы:
— В параллелограмме \(BCC_1C\) противоположные стороны равны, следовательно, \(BC = AD\) и \(CC_1 = AA_1\).
4) Подставим выражения из пункта 2 в пункт 1:
\[ AC_1 < (AB + BC) + CC_1 \]
5) Заменим \(BC\) на \(AD\) и \(CC_1\) на \(AA_1\) из свойства параллелограмма:
\[ AC_1 < AB + AD + AA_1 \]
Таким образом, мы показали, что \(AC_1 < AB + AD + AA_1\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!