ГДЗ по Геометрии 9 класс Номер 1224 Атанасян — Подробные Ответы

Докажите, что объём шара радиуса \( R \) равен \(\frac{4}{3} \pi R^3\).

Решение

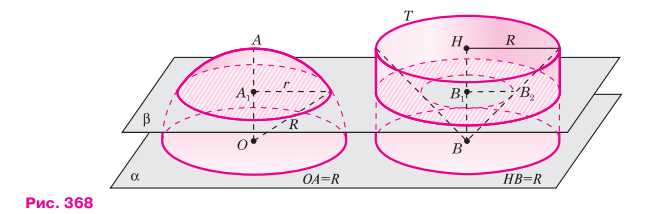
Рассмотрим два тела: половину шара радиуса \( R \) и тело \( T \), представляющее собой цилиндр радиуса \( R \) с высотой \( R \), из которого вырезан конус с радиусом основания и высотой \( R \). Представим себе, что оба тела стоят на плоскости \(\alpha\) так, как показано на рисунке 368. Проведём секущую плоскость \(\beta\), параллельную плоскости \(\alpha\) и пересекающую радиус шара \( OA \), перпендикулярный к плоскости \(\alpha\), в точке \( A_1 \), а высоту \( BH \) конуса — в точке \( B_1 \).

Сечение половины шара представляет собой круг радиуса \(\sqrt{R^2 — OA_1^2}\) (см. рис. 368). Поэтому площадь этого круга равна \(\pi (R^2 — OA_1^2)\).

Сечение тела \( T \) представляет собой кольцо, площадь которого равна разности площадей двух кругов: круга радиуса \( R \) и круга радиуса \( B_1B_2 \) (см. рис. 368), т. е. равна \(\pi (R^2 — B_1B_2^2)\). Но \( B_1B_2 = BB_1 \) (объясните почему) и, кроме того, \( BB_1 = OA_1 \) (доказательство этого наглядно очевидного факта будет приведено в курсе стереометрии 10—11 классов).

Таким образом, площадь сечения половины шара равна площади сечения тела \( T \). Поэтому и объём половины шара равен объёму этого тела. В свою очередь, объём \( V \) тела \( T \) можно вычислить как разность объёмов цилиндра и конуса:

\[ V = \pi R^2 \cdot R — \frac{1}{3} \pi R^2 \cdot R = \frac{2}{3} \pi R^3. \]

Итак, объём половины шара равен \(\frac{2}{3} \pi R^3\) и, следовательно, объём всего шара равен \(\frac{4}{3} \pi R^3\).

Доказать: Объем шара радиуса \(R\) равен \(\frac{4}{3}\pi R^3\);

Доказательство:

1) Рассмотрим два тела: половину шара радиуса \(R\) и тело \(T\) — цилиндр радиуса \(R\) с высотой \(R\), из которого вырезан конус с радиусом основания и высотой \(R\);
2) Пусть оба тела опираются на плоскость \(\alpha\), проведем плоскость \(\beta \perp \alpha\) и пересекающую радиус шара \(OA\), перпендикулярный к плоскости \(\alpha\), в точке \(A_1\), а высоту \(BH\) конуса — в точке \(B_1\);
3) Сечение половины шара представляет собой круг радиуса \(\sqrt{R^2 — OA_1^2}\), значит площадь этого круга равна \(\pi(R^2 — OA_1^2)\);
4) Сечение тела \(T\) представляет собой кольцо, площадь которого равна разности площадей двух кругов: круга радиуса \(R\) и круга радиуса \(B_1B_2\), то есть равна \(\pi(R^2 — B_1B_2^2)\);
5) \(B_1B_2 = BB_1\) (так как \(BB_1 = R\), \(B_1B_2 = R\)) и \(BB_1 = OA_1\), значит площадь сечения половины шара равна площади сечения тела \(T\), следовательно и объем половины шара равен объему этого тела;
6) \(V_T = \pi R^2 \cdot R — \frac{1}{3}\pi R^2 \cdot R = \frac{2}{3}\pi R^3\);
7) Отсюда \(V_{\text{шара}} = 2 \times \frac{2}{3}\pi R^3 = \frac{4}{3}\pi R^3\), что и требовалось доказать.

Докажем, что объём шара радиуса \( R \) равен \(\frac{4}{3} \pi R^3\).

Для этого рассмотрим два тела: половину шара радиуса \( R \) и тело \( T \), представляющее собой цилиндр радиуса \( R \) с высотой \( R \), из которого вырезан конус с радиусом основания и высотой \( R \).

Предположим, что оба тела стоят на плоскости \(\alpha\). Проведём секущую плоскость \(\beta\), параллельную плоскости \(\alpha\) и пересекающую радиус шара \( OA \), перпендикулярный к плоскости \(\alpha\), в точке \( A_1 \), а высоту \( BH \) конуса — в точке \( B_1 \).

Сечение половины шара представляет собой круг радиуса \(\sqrt{R^2 — OA_1^2}\). Поэтому площадь этого круга равна \(\pi (R^2 — OA_1^2)\).

Сечение тела \( T \) представляет собой кольцо, площадь которого равна разности площадей двух кругов: круга радиуса \( R \) и круга радиуса \( B_1B_2 \). То есть, площадь равна \(\pi (R^2 — B_1B_2^2)\).

Заметим, что \( B_1B_2 = BB_1 \) и \( BB_1 = OA_1 \). Это объясняется тем, что \( BB_1 \) и \( OA_1 \) — это высоты соответствующих треугольников, равных по гипотенузе и одному из катетов.

Таким образом, площадь сечения половины шара равна площади сечения тела \( T \). Следовательно, объём половины шара равен объёму тела \( T \).

Теперь вычислим объём \( V \) тела \( T \) как разность объёмов цилиндра и конуса:

1. Объём цилиндра: \( V_{\text{цилиндра}} = \pi R^2 \cdot R = \pi R^3 \).
2. Объём конуса: \( V_{\text{конуса}} = \frac{1}{3} \pi R^2 \cdot R = \frac{1}{3} \pi R^3 \).

Тогда объём тела \( T \):

\[ V = \pi R^3 — \frac{1}{3} \pi R^3 = \frac{2}{3} \pi R^3. \]

Таким образом, объём половины шара равен \(\frac{2}{3} \pi R^3\). Следовательно, объём всего шара равен:

\[ 2 \times \frac{2}{3} \pi R^3 = \frac{4}{3} \pi R^3. \]

Это и требовалось доказать.