ГДЗ по Геометрии 9 класс Номер 1223 Атанасян — Подробные Ответы

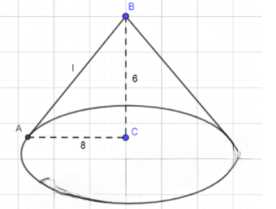
Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей образованного при этом вращении ко нуса.

Дано: \(\triangle ABC\); \(\angle C = 90^\circ\); \(AC = 8 \, \text{см}\); \(BC = 6 \, \text{см}\); Конус(\(AC; BC\)); Найти: \(S_{\text{бок}}\), \(S_{\text{полн}} — ?\);

Решение:

1) Найдем образующую конуса:
\(l = AB = \sqrt{AC^2 + BC^2} = \sqrt{8^2 + 6^2} = 10 \, \text{см}\);

2) Найдем площадь боковой поверхности:
\(S_{\text{бок}} = \pi r l = \pi \cdot AC \cdot AB = \pi \cdot 8 \cdot 10 = 80\pi \, \text{см}^2\);

3) Найдем площадь основания:
\(S_{\text{осн}} = \pi r^2 = \pi \cdot AC^2 = 64\pi \, \text{см}^2\);

4) \(S = S_{\text{бок}} + S_{\text{осн}} = 80\pi + 64\pi = 144\pi \, \text{см}^2\);

Ответ: \(S_{\text{бок}} = 80\pi \, \text{см}^2\); \(S = 144\pi \, \text{см}^2\).

Дано: \(\triangle ABC\); \(\angle C = 90^\circ\); \(AC = 8 \, \text{см}\); \(BC = 6 \, \text{см}\); Конус(\(AC; BC\)). Найти: \(S_{\text{бок}}\), \(S_{\text{полн}}\).

Решение:

1) Найдем длину гипотенузы \(AB\), которая является образующей конуса \(l\). Используем теорему Пифагора:

\(
l = AB = \sqrt{AC^2 + BC^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10 \, \text{см}
\)

2) Найдем площадь боковой поверхности конуса \(S_{\text{бок}}\). Формула для площади боковой поверхности конуса:

\(
S_{\text{бок}} = \pi \cdot r \cdot l
\)

где \(r = AC = 8 \, \text{см}\), \(l = 10 \, \text{см}\). Подставим значения:

\(
S_{\text{бок}} = \pi \cdot 8 \cdot 10 = 80\pi \, \text{см}^2
\)

3) Найдем площадь основания конуса \(S_{\text{осн}}\). Основание конуса — это круг с радиусом \(r = AC = 8 \, \text{см}\). Формула для площади круга:

\(
S_{\text{осн}} = \pi \cdot r^2 = \pi \cdot 8^2 = 64\pi \, \text{см}^2
\)

4) Найдем полную поверхность конуса \(S_{\text{полн}}\), которая равна сумме площади боковой поверхности и площади основания:

\(
S_{\text{полн}} = S_{\text{бок}} + S_{\text{осн}} = 80\pi + 64\pi = 144\pi \, \text{см}^2
\)

Ответ: \(S_{\text{бок}} = 80\pi \, \text{см}^2\); \(S_{\text{полн}} = 144\pi \, \text{см}^2\).