ГДЗ по Геометрии 9 класс Номер 1221 Атанасян — Подробные Ответы

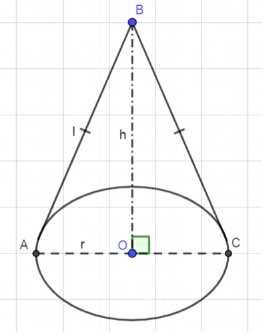
Найдите объём конуса, если площадь его основания равна Q, а площадь боковой поверхности равна Р.

Дано:
ABC — конус;
\(S_{OCH} = Q\);
\(S_{бок} = P\);

Найти: \(V\) — ?;

Решение:
1) \(V = \frac{1}{3} \pi r^2 h\), где \(r\) — радиус основания, \(h\) — высота;
2) По условию \(S_{OCH} = Q\), также \(S_{OCH} = \pi r^2\), значит
\(\pi r^2 = Q \Rightarrow r^2 = \frac{Q}{\pi}\), откуда \(r = \sqrt{\frac{Q}{\pi}}\);
3) \(S_{бок} = \pi rl\), где \(l = AB\) — образующая конуса;
Так как \(S_{бок} = P\), то \(\pi rl = P\), откуда:
\(l = \frac{P}{\pi r} = \frac{P}{\pi \sqrt{\frac{Q}{\pi}}} = \frac{P}{\sqrt{\pi Q}}\);
4) Рассмотрим \(\triangle AOB\) — прямоугольный:
\(h = \sqrt{l^2 — r^2} = \sqrt{\frac{P^2}{\pi Q} — \frac{Q}{\pi}} = \sqrt{\frac{P^2 — Q^2}{\pi Q}}\);
5) \(V = \frac{1}{3} \cdot Q \cdot \sqrt{\frac{P^2 — Q^2}{\pi Q}} = \frac{1}{3} \cdot \sqrt{\frac{Q (P^2 — Q^2)}{\pi}}\);

Ответ: \(\frac{1}{3} \sqrt{\frac{Q (P^2 — Q^2)}{\pi}}\).

Дано:
ABC — конус;
\(S_{OCH} = Q\);
\(S_{бок} = P\);

Найти: \(V\) — ?;

Решение:

1) Объем конуса \(V\) находится по формуле:

\(
V = \frac{1}{3} \pi r^2 h
\)

где \(r\) — радиус основания, \(h\) — высота конуса.

2) По условию задачи, площадь основания конуса \(S_{OCH} = Q\). Площадь основания также выражается через радиус:

\(
S_{OCH} = \pi r^2
\)

Отсюда:

\(
\pi r^2 = Q \Rightarrow r^2 = \frac{Q}{\pi}
\)

Следовательно, радиус равен:

\(
r = \sqrt{\frac{Q}{\pi}}
\)

3) Площадь боковой поверхности конуса \(S_{бок}\) выражается через радиус и образующую \(l\):

\(
S_{бок} = \pi r l
\)

По условию, \(S_{бок} = P\), значит:

\(
\pi r l = P
\)

Отсюда находим образующую:

\(
l = \frac{P}{\pi r} = \frac{P}{\pi \sqrt{\frac{Q}{\pi}}} = \frac{P}{\sqrt{\pi Q}}
\)

4) Рассмотрим прямоугольный треугольник \(\triangle AOB\), где \(h\) — высота, \(r\) — радиус, \(l\) — гипотенуза (образующая). По теореме Пифагора:

\(
h = \sqrt{l^2 — r^2}
\)

Подставляем найденные выражения для \(l\) и \(r\):

\(
h = \sqrt{\left(\frac{P}{\sqrt{\pi Q}}\right)^2 — \left(\sqrt{\frac{Q}{\pi}}\right)^2} = \sqrt{\frac{P^2}{\pi Q} — \frac{Q}{\pi}}
\)

Приводим под общий знаменатель:

\(
h = \sqrt{\frac{P^2 — Q^2}{\pi Q}}
\)

5) Подставляем выражения для \(r\) и \(h\) в формулу объема:

\(
V = \frac{1}{3} \pi \left(\sqrt{\frac{Q}{\pi}}\right)^2 \cdot \sqrt{\frac{P^2 — Q^2}{\pi Q}}
\)

Упрощаем:

\(
V = \frac{1}{3} \cdot Q \cdot \sqrt{\frac{P^2 — Q^2}{\pi Q}}
\)

\(
V = \frac{1}{3} \cdot \sqrt{\frac{Q (P^2 — Q^2)}{\pi}}
\)

Ответ: \(\frac{1}{3} \cdot \sqrt{\frac{Q (P^2 — Q^2)}{\pi}}\).