ГДЗ по Геометрии 9 класс Номер 1219 Атанасян — Подробные Ответы

Докажите, что объём конуса равен одной трети произведения площади основания на высоту.
Решение
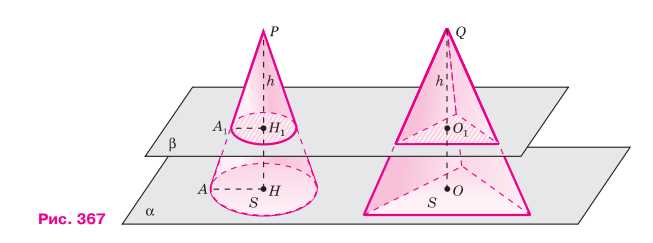
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований \(S\) и высотами \(PH = h\) и \(QO = h\) соответственно, стоящие на одной плоскости \(\alpha\) (рис. 367). Докажем, что объём конуса равен \(\frac{1}{3} Sh\).
Проведём секущую плоскость \(\beta\), параллельную плоскости \(\alpha\) и пересекающую высоты \(PH\) и \(QO\) в точках \(H_1\) и \(O_1\) соответственно. В сечении конуса плоскостью \(\beta\) получится круг радиуса \(H_1A_1\). Треугольники \(PH_1A_1\) и \(PHA\) подобны по двум углам (\(\angle P\) — общий, \(\angle PH_1A_1 = \angle PHA = 90^\circ\), так как в противном случае прямые \(HA\) и \(H_1A_1\), а значит, и плоскости \(\alpha\) и \(\beta\) пересекались бы, что противоречит условию). Поэтому \(
\frac{H_1A_1}{HA} = \frac{PH_1}{PH}
\) откуда \(
H_1A_1 = \frac{PH_1}{PH} \cdot HA
\) и площадь сечения конуса равна \(
\pi(H_1A_1)^2 = \left(\frac{PH_1}{PH}\right)^2 \cdot \pi HA^2 = \left(\frac{PH_1}{PH}\right)^2 \cdot S.
\)

Площадь сечения пирамиды равна

\(
\left(\frac{QO_1}{QO}\right)^2 \cdot S
\)

(см. задачу 1209). По условию \(PH = QO = h\). Интуитивно ясно также, что \(PH_1 = QO_1\) (строгое доказательство этого факта будет дано в курсе стереометрии 10–11 классов). Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объём равен объёму пирамиды, т. е. равен \(\frac{1}{3} Sh\), что и требовалось доказать.

Доказать: объем конуса равен одной трети произведения площади основания на высоту;

Доказательство:

1) Воспользуемся принципом Кавальери:
Рассмотрим конус и пирамиду с площадями оснований \(S\) и высотами \(PH = h\) и \(QO = h\) соответственно, стоящие на одной плоскости \(\alpha\). Докажем, что объем конуса равен \(\frac{1}{3} Sh\);

2) Проведем секущую плоскость \(\beta\), параллельную плоскости \(\alpha\) и пересекающую высоты \(PH\) и \(PQ\) в точках \(H_1\) и \(O_1\) соответственно;

3) В сечении конуса плоскостью \(\beta\) получится круг радиуса \(H_1A_1\); Треугольники \(PH_1A_1\) и \(PHA\) подобны по двум углам (\(\angle P\) — общий, \(\angle PH_1A_1 = \angle PHA = 90^\circ\)), следовательно: \(
\frac{H_1A_1}{HA} = \frac{PH_1}{PH}
\) откуда \(
H_1A_1 = \frac{PH_1}{PH} \cdot HA
\) и площадь сечения конуса равна:

\(
\pi(H_1A_1)^2 = \pi \left(\frac{PH_1}{PH} \cdot HA\right)^2 = \left(\frac{PH_1}{PH}\right)^2 \cdot \pi HA^2 = \left(\frac{PH_1}{PH}\right)^2 \cdot S
\)

4) Площадь сечения пирамиды равна \(\left(\frac{GO_1}{GO}\right)^2 \cdot S\);

5) Следовательно, площади сечения пирамиды и конуса равны, а значит и объем равен \(\frac{1}{3} Sh\), что и требовалось доказать.

Докажите, что объём конуса равен одной трети произведения площади основания на высоту.

Решение
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований \(S\) и высотами \(PH = h\) и \(QO = h\) соответственно, стоящие на одной плоскости \(\alpha\). Докажем, что объём конуса равен \(\frac{1}{3} Sh\).

Проведём секущую плоскость \(\beta\), параллельную плоскости \(\alpha\) и пересекающую высоты \(PH\) и \(QO\) в точках \(H_1\) и \(O_1\) соответственно. В сечении конуса плоскостью \(\beta\) получится круг радиуса \(H_1A_1\). Треугольники \(PH_1A_1\) и \(PHA\) подобны по двум углам (\(\angle P\) — общий, \(\angle PH_1A_1 = \angle PHA = 90^\circ\)), следовательно:

\(
\frac{H_1A_1}{HA} = \frac{PH_1}{PH}
\) откуда \(
H_1A_1 = \frac{PH_1}{PH} \cdot HA
\) и площадь сечения конуса равна:

\(
\pi(H_1A_1)^2 = \pi \left(\frac{PH_1}{PH} \cdot HA\right)^2 = \left(\frac{PH_1}{PH}\right)^2 \cdot \pi HA^2 = \left(\frac{PH_1}{PH}\right)^2 \cdot S
\)

Площадь сечения пирамиды равна:

\(
\left(\frac{QO_1}{QO}\right)^2 \cdot S
\)

Теперь, чтобы доказать равенство объёмов, воспользуемся следующим рассуждением. Поскольку площади сечений конуса и пирамиды на любой высоте \(x\) одинаковы, то по принципу Кавальери их объёмы также равны. Для конуса:

\(
V_{\text{конуса}} = \int_0^h \pi \left(\frac{x}{h}\right)^2 \cdot S \, dx
\)

Рассчитаем интеграл:

\(
V_{\text{конуса}} = \pi S \int_0^h \left(\frac{x}{h}\right)^2 \, dx = \pi S \cdot \frac{1}{h^2} \int_0^h x^2 \, dx
\)

Вычислим \(\int_0^h x^2 \, dx\):

\(
\int_0^h x^2 \, dx = \left(\frac{x^3}{3}\right)_0^h = \frac{h^3}{3}
\)

Таким образом:

\(
V_{\text{конуса}} = \pi S \cdot \frac{1}{h^2} \cdot \frac{h^3}{3} = \frac{1}{3} \pi Sh
\)

Следовательно, объём конуса равен \(\frac{1}{3} Sh\), что и требовалось доказать.